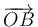Cuestión de álgebra vectorial, Noviembre 2011
De Laplace
(Diferencias entre revisiones)
(→Enunciado) |
(→Longitud de la diagonal) |
||
| Línea 14: | Línea 14: | ||
<center><math>\vec{c}=\vec{a}+\vec{b}</math></center> | <center><math>\vec{c}=\vec{a}+\vec{b}</math></center> | ||
| + | |||
| + | La longitud de la diagonal <math>OC</math> es el módulo de este vector, | ||
| + | |||
| + | <center><math>|\overrightarrow{OC}|=|\vec{c}|=\sqrt{\vec{c}\cdot\vec{c}}\mathrm{,}</math></center> | ||
| + | |||
| + | que podemos obtener a partir del producto escalar del vector por sí mismo: | ||
| + | |||
| + | <center><math>\vec{c}\cdot\vec{c}=(\vec{a}+\vec{b})\cdot(\vec{a}+\vec{b})=\vec{a}\cdot\vec{a}+2\vec{a}\cdot\vec{b}+\vec{b}\cdot\vec{b}</math></center> | ||
| + | |||
| + | Como los lados <math>OA</math> y <math>OB</math> tienen longitud unidad, sus correspondientes vectores tienen módulo 1. Se tendrán entonces, | ||
| + | |||
| + | <center><math>\vec{c}\cdot\vec{c}=|\vec{a}|^2+2|\vec{a}||\vec{b}|\cos \theta+|\vec{b}|^2=2+2\cos\theta\mathrm{,}</math></center> | ||
| + | siendo <math>\theta</math> el ángulo que forman los segmentos <math>\overrightarrow{OA}</math> y <math>\overrightarrow{OB}</math> | ||
Revisión de 12:26 20 nov 2011
1 Enunciado
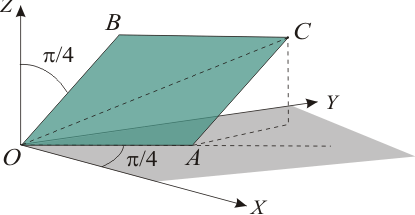
El rombo OACB tiene sus lados de longitud unidad y suárea es igual a 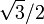 . Su lado OA se encuentra en el plano
OXY de un sistema de referencia cartesiano, formando un ángulo de
π / 4 con el eje OX. El lado OB forma un ángulo de π / 4
con el eje OZ.
. Su lado OA se encuentra en el plano
OXY de un sistema de referencia cartesiano, formando un ángulo de
π / 4 con el eje OX. El lado OB forma un ángulo de π / 4
con el eje OZ.
- Calcular la longitud de la diagonal OC
- Determinar las coordenads cartesianas del vértice C
2 Solución
2.1 Longitud de la diagonal
Consideremos los vectores  ,
,  y
y 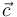 , de igual módulo, dirección y sentido que los respectivos segmentos orientados
, de igual módulo, dirección y sentido que los respectivos segmentos orientados  ,
, 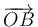 y
y  . Al corresponder éstos con dos lados adyacentes y la diagonal del rombo, se tendrán que
. Al corresponder éstos con dos lados adyacentes y la diagonal del rombo, se tendrán que
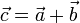
La longitud de la diagonal OC es el módulo de este vector,
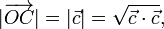
que podemos obtener a partir del producto escalar del vector por sí mismo:
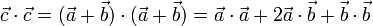
Como los lados OA y OB tienen longitud unidad, sus correspondientes vectores tienen módulo 1. Se tendrán entonces,
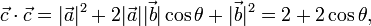
siendo θ el ángulo que forman los segmentos  y
y