Masa girando alrededor de una mano
De Laplace
(→Solución) |
|||
| Línea 23: | Línea 23: | ||
<center><math>m\vec{a}=-m\omega^2 R\vec{u}_\rho</math></center> | <center><math>m\vec{a}=-m\omega^2 R\vec{u}_\rho</math></center> | ||
| - | aquí <math>R</math> no es la longitud de la cuerda, sino el radio de la circunferencia. Este se relaciona con la longitud por | + | aquí <math>R</math> no es la longitud de la cuerda, sino el radio de la circunferencia. Este se relaciona con la longitud <math>b</math> de la cuerda por |
| - | <center><math>R = | + | <center><math>R = b\cos(\phi)\,</math></center> |
La velocidad angular la hallamos sabiendo que el enunciado nos da la frecuencia natural (2 vueltas por segundo, esto es 2 Hz). | La velocidad angular la hallamos sabiendo que el enunciado nos da la frecuencia natural (2 vueltas por segundo, esto es 2 Hz). | ||
| Línea 31: | Línea 31: | ||
Sustituyendo todo esto en la ecuación de movimiento queda | Sustituyendo todo esto en la ecuación de movimiento queda | ||
| - | <center><math>-mg\vec{k}+F_T\left(-\cos(\phi)\vec{u}_\rho+\mathrm{sen}(\phi)\vec{k}\right)=-m\omega^ | + | <center><math>-mg\vec{k}+F_T\left(-\cos(\phi)\vec{u}_\rho+\mathrm{sen}(\phi)\vec{k}\right)=-m\omega^2b\cos(\phi)\vec{u}_\rho</math></center> |
Igualando componente a componente | Igualando componente a componente | ||
| - | <center><math>\left\{\begin{array}{rcl}-F_T\cos(\phi) & = & -m\omega^ | + | <center><math>\left\{\begin{array}{rcl}-F_T\cos(\phi) & = & -m\omega^2b\cos(\phi) \\ && \\ -mg+F_T\mathrm{sen}(\phi) & = & 0\end{array}\right.</math></center> |
De la primera de estas dos obtenemos la tensión | De la primera de estas dos obtenemos la tensión | ||
| - | <center><math>F_T = m\omega^2 | + | <center><math>F_T = m\omega^2 b\,</math></center> |
y, conocida la tensión, hallamos el ángulo con la horizontal | y, conocida la tensión, hallamos el ángulo con la horizontal | ||
| - | <center><math>\mathrm{sen}(\phi) = \frac{mg}{F_T}=\frac{g}{\omega^ | + | <center><math>\mathrm{sen}(\phi) = \frac{mg}{F_T}=\frac{g}{\omega^2b}</math></center> |
Vemos que el ángulo es independiente de la masa de la bola, y que existe un valor inferior para la velocidad angular, ya que si es demasiado baja implicaría un seno mayor que la unidad, lo que no es posible. | Vemos que el ángulo es independiente de la masa de la bola, y que existe un valor inferior para la velocidad angular, ya que si es demasiado baja implicaría un seno mayor que la unidad, lo que no es posible. | ||
última version al 17:24 26 nov 2014
1 Enunciado
Una masa de 0.5 kg situada en el extremo de una cuerda de 50 cm de longitud se hace girar horizontalmente con la mano de manera que da 2 vueltas por segundo. ¿Puede estar la cuerda completamente horizontal? Determine la tensión de la cuerda y el ángulo que forma con la horizontal.

2 Solución
La masa realiza su movimiento circular como consecuencia de la acción de dos fuerzas: su peso y la tensión de la cuerda
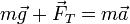
El peso va en la dirección vertical
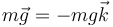
mientras que la tensión va en la dirección de la cuerda y por tanto tiene una componente radial hacia adentro y otra vertical hacia arriba. Si φ es el ángulo que el hilo forma con la horizontal, la tensión se escribe

Por último, la aceleración en un movimiento circular uniforme es puramente radial y hacia adentro, siendo su módulo proporcional al radio de la circunferencia y al cuadrado de la velocidad angular

aquí R no es la longitud de la cuerda, sino el radio de la circunferencia. Este se relaciona con la longitud b de la cuerda por
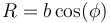
La velocidad angular la hallamos sabiendo que el enunciado nos da la frecuencia natural (2 vueltas por segundo, esto es 2 Hz).
Sustituyendo todo esto en la ecuación de movimiento queda
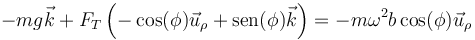
Igualando componente a componente
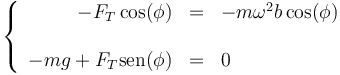
De la primera de estas dos obtenemos la tensión
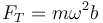
y, conocida la tensión, hallamos el ángulo con la horizontal

Vemos que el ángulo es independiente de la masa de la bola, y que existe un valor inferior para la velocidad angular, ya que si es demasiado baja implicaría un seno mayor que la unidad, lo que no es posible.
Sustituyendo los valores del enunciado obtenemos el valor numérico de la velocidad angular
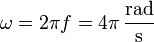
la tensión
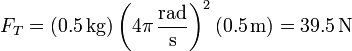
y el ángulo con la horizontal.







