2.5. Rectilíneo con desaceleración creciente (Ex.Nov/11)
De Laplace
(Diferencias entre revisiones)
(Página creada con '==Enunciado== Categoría:Problemas de cinemática del punto material (G.I.T.I.)') |
(→Enunciado) |
||
| Línea 1: | Línea 1: | ||
==Enunciado== | ==Enunciado== | ||
| + | Una partícula está recorriendo el eje OX en sentido positivo con una celeridad constante de 25 m/s. En un instante dado (t=0) se detecta un obstáculo en su trayectoria a 50 m por delante de ella. A partir de dicho instante se le aplica a la partícula una desaceleración creciente en el tiempo según la fórmula <math>\,\vec{a}(t)=-Kt\,\vec{\imath}\,\,</math>, donde <math>K\,</math> es una constante de valor igual a 8.00 m/s<math>^{3}</math>. ¿Cuánto tiempo tardará en detenerse la partícula? ¿A qué distancia del obstáculo se detendrá? | ||
[[Categoría:Problemas de cinemática del punto material (G.I.T.I.)]] | [[Categoría:Problemas de cinemática del punto material (G.I.T.I.)]] | ||
Revisión de 01:04 12 nov 2011
Enunciado
Una partícula está recorriendo el eje OX en sentido positivo con una celeridad constante de 25 m/s. En un instante dado (t=0) se detecta un obstáculo en su trayectoria a 50 m por delante de ella. A partir de dicho instante se le aplica a la partícula una desaceleración creciente en el tiempo según la fórmula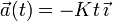 
, donde 
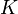es una constante de valor igual a 8.00 m/s3. ¿Cuánto tiempo tardará en detenerse la partícula? ¿A qué distancia del obstáculo se detendrá?
