1.9. Longitud de una sombra (Ex.Nov/11)
De Laplace
(→Solución) |
m (Longitud de una sombra trasladada a Longitud de una sombra (Ex.Nov/11)) |
Revisión de 12:30 14 nov 2011
1 Enunciado
En cierto sistema de coordenadas cartesianas, el suelo viene definido por el plano de ecuación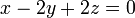 
y en él se halla clavada una varilla rectilínea representada por el vector 
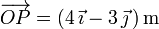. Suponiendo que es mediodía y los rayos solares inciden
perpendicularmente al suelo, ¿cuál es la longitud de la sombra que la varilla proyecta sobre el suelo?
2 Solución
Por inspección de la ecuación del plano-suelo, deducimos de inmediato un vector 
normal al suelo, y dividiéndolo por su módulo (normalización) obtenemos un vector unitario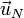 
en su misma dirección:
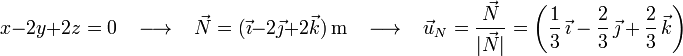
Pues bien, la sombra de la varilla sobre el suelo al mediodía (incidencia ortogonal de los rayos solares) es la proyección ortogonal del vector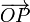 
sobre el plano-suelo, es decir, su proyección sobre la dirección perpendicular al vector . Por tanto, la longitud 
de dicha sombra se puede calcular como el módulo del producto vectorial del vector 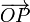por el vector unitario en la dirección normal al suelo :
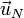![L=\mathrm{proy}_{\perp \vec{N}}\left[\overrightarrow{OP}\right]=\left|\overrightarrow{OP}\times\vec{u}_N\right|=\left|-2\,\vec{\imath}-\frac{8}{3}\,\vec{\jmath}-\frac{5}{3}\,\vec{k}\,\right|\,\mathrm{m}=\sqrt{\frac{125}{9}}\,\mathrm{m}=\frac{5\sqrt{5}}{3}\,\mathrm{m}](/wiki/images/math/7/b/4/7b4c467da51fb01f52e48478ce78e9cb.png)
