1.3. Lados de un triángulo rectángulo (Ex.Nov/11)

De Laplace

(Diferencias entre revisiones)

Revisión de 09:24 10 nov 2011

1 Enunciado

¿Cuál de las siguientes ternas de vectores libres podría corresponder a los tres lados de un triángulo rectángulo?

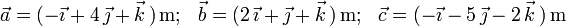
1) $\,\,\,\vec{a}=(-\vec{\imath}+4\,\vec{\jmath}+\vec{k}\,)\,\mathrm{m;}\,\,\,\,\, \vec{b}=(2\,\vec{\imath}+\vec{\jmath}+\vec{k}\,)\,\mathrm{m;}\,\,\,\,\, \vec{c}=(-\vec{\imath}-5\,\vec{\jmath}-2\,\vec{k}\,)\,\mathrm{m}\,$

2) $\,\,\,\vec{a}=(3\,\vec{\imath}+2\,\vec{k}\,)\,\mathrm{m;}\,\,\,\,\, \vec{b}=(2\,\vec{\imath}-3\,\vec{k}\,)\,\mathrm{m;}\,\,\,\,\, \vec{c}=(5\,\vec{\imath}+\vec{k}\,)\,\mathrm{m}\,$

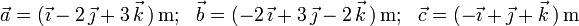
3) $\,\,\,\vec{a}=(\vec{\imath}-2\,\vec{\jmath}+3\,\vec{k}\,)\,\mathrm{m;}\,\,\,\,\, \vec{b}=(-2\,\vec{\imath}+3\,\vec{\jmath}-2\,\vec{k}\,)\,\mathrm{m;}\,\,\,\,\, \vec{c}=(-\vec{\imath}+\vec{\jmath}+\vec{k}\,)\,\mathrm{m}\,$

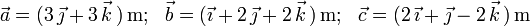
4) $\,\,\,\vec{a}=(3\,\vec{\jmath}+3\,\vec{k}\,)\,\mathrm{m;}\,\,\,\,\, \vec{b}=(\vec{\imath}+2\,\vec{\jmath}+2\,\vec{k}\,)\,\mathrm{m;}\,\,\,\,\, \vec{c}=(2\,\vec{\imath}+\vec{\jmath}-2\,\vec{k}\,)\,\mathrm{m}\,$

2 Solución

Lo primero que se debe comprobar es cuáles de esas ternas podrían corresponder realmente a un triángulo. Teniendo en cuenta que un triángulo es una figura geométrica cerrada...

@@ Línea 19: / Línea 19: @@
 ==Solución==
+Lo primero que se debe comprobar es cuáles de esas ternas podrían corresponder realmente a un triángulo. Teniendo en cuenta que un triángulo es una figura geométrica cerrada...
 [[Categoría:Problemas de vectores libres (G.I.T.I.)]]

1.3. Lados de un triángulo rectángulo (Ex.Nov/11)

De Laplace

Revisión de 09:24 10 nov 2011

1 Enunciado

2 Solución

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES