1.2. Ecuación dimensional de G (Ex.Nov/11)
De Laplace
(Diferencias entre revisiones)
(→Enunciado) |
(→Solución) |
||
| Línea 9: | Línea 9: | ||
==Solución== | ==Solución== | ||
| + | Sabemos que la fuerza se define como la derivada de la cantidad de movimiento con respecto al tiempo (aunque también suele expresarse como el producto de la masa por la aceleración). Por ello | ||
| + | <center><math>[F] = \frac{[p]}{[t]} = \frac{MLT^{-1}}{T}=MLT^{-2}</math></center> | ||
[[Categoría:Problemas de metrología (G.I.T.I.)]] | [[Categoría:Problemas de metrología (G.I.T.I.)]] | ||
Revisión de 15:50 8 nov 2011
1 Enunciado
La ley de la Gravitación Universal establece que la interacción gravitatoria entre dos cuerpos puede expresarse mediante una fuerza
cuyo módulo es directamente proporcional al producto de las masas de los cuerpos (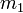
y 
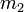) e inversamente proporcional al cuadrado de la distancia (
) que los separa, es decir:
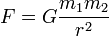
¿Cuál es la ecuación dimensional de la constante de gravitación
universal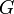 
en el SI?
2 Solución
Sabemos que la fuerza se define como la derivada de la cantidad de movimiento con respecto al tiempo (aunque también suele expresarse como el producto de la masa por la aceleración). Por ello
![[F] = \frac{[p]}{[t]} = \frac{MLT^{-1}}{T}=MLT^{-2}](/wiki/images/math/8/6/9/869bb07dc26bc625d804a015bb338ed7.png)
