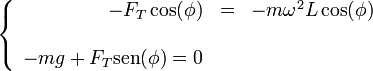Masa girando alrededor de una mano
De Laplace
(Página creada con '==Enunciado== Una masa de 0.5 kg situada en el extremo de una cuerda de 50 cm de longitud se hace girar horizontalmente con la mano de manera que da 2 vueltas por…') |
|||
| Línea 3: | Línea 3: | ||
<center>[[Archivo:mano-hilo-pesa.jpg]]</center> | <center>[[Archivo:mano-hilo-pesa.jpg]]</center> | ||
| + | |||
| + | ==Solución== | ||
| + | La masa realiza su movimiento circular como consecuencia de la acción de dos fuerzas: su peso y la tensión de la cuerda | ||
| + | |||
| + | <center><math>m\vec{g}+\vec{F}_T = m\vec{a}</math></center> | ||
| + | |||
| + | El peso va en la dirección vertical | ||
| + | |||
| + | <center><math>m\vec{g}=-mg\vec{k}</math></center> | ||
| + | |||
| + | mientras que la tensión va en la dirección de la cuerda y por tanto tiene una componente radial hacia adentro y otra vertical hacia arriba. Si <math>\phi</math> es el ángulo que el hilo forma con la horizontal, la tensión se escribe | ||
| + | |||
| + | <center><math>\vec{F}_T = F_T\left(-\cos(\phi)\vec{u}_\rho+\mathrm{sen}(\phi)\vec{k})</math></center> | ||
| + | |||
| + | Por último, la aceleración en un movimiento circular uniforme es puramente radial y hacia adentro, siendo su módulo proporcional al radio de la circunferencia y al cuadrado de la velocidad angular | ||
| + | |||
| + | <center><math>m\vec{a}=-m\omega^2 R\vec{u}_\rho</math></center> | ||
| + | |||
| + | aquí <math>R</math> no es la longitud de la cuerda, sino el radio de la circunferencia. Este se relaciona con la longitud por | ||
| + | |||
| + | <center><math>R = L\cos(\phi)\,</math></center> | ||
| + | |||
| + | Sustituyendo todo es to en la ecuación de movimiento queda | ||
| + | |||
| + | <center><math>-mg\vec{k}+F_T\left(-\cos(\phi)\vec{u}_\rho+\mathrm{sen}(\phi)\vec{k})=-m\omega^2L\cos(\phi)\vec{u}_\rho</math></center> | ||
| + | |||
| + | Igualando componente a componente | ||
| + | |||
| + | <center><math>\left\{\begin{array}{rcl}-F_T\cos(\phi) & = & -m\omega^2L\cos(\phi) \\ && \\ -mg+F_T\mathrm{sen}(\phi)=0\end{array}\right.</math></center> | ||
[[Categoría:Problemas de dinámica de la partícula (GIE)]] | [[Categoría:Problemas de dinámica de la partícula (GIE)]] | ||
Revisión de 22:01 12 nov 2011
1 Enunciado
Una masa de 0.5 kg situada en el extremo de una cuerda de 50 cm de longitud se hace girar horizontalmente con la mano de manera que da 2 vueltas por segundo. ¿Puede estar la cuerda completamente horizontal? Determine la tensión de la cuerda y el ángulo que forma con la horizontal.

2 Solución
La masa realiza su movimiento circular como consecuencia de la acción de dos fuerzas: su peso y la tensión de la cuerda
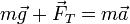
El peso va en la dirección vertical
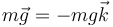
mientras que la tensión va en la dirección de la cuerda y por tanto tiene una componente radial hacia adentro y otra vertical hacia arriba. Si φ es el ángulo que el hilo forma con la horizontal, la tensión se escribe
Por último, la aceleración en un movimiento circular uniforme es puramente radial y hacia adentro, siendo su módulo proporcional al radio de la circunferencia y al cuadrado de la velocidad angular

aquí R no es la longitud de la cuerda, sino el radio de la circunferencia. Este se relaciona con la longitud por

Sustituyendo todo es to en la ecuación de movimiento queda
Igualando componente a componente