Variación de la presión atmosférica
De Laplace
(Página creada con '==Enunciado== La presión atmosférica en un punto se debe al peso por unidad de superficie de la columna de aire situada sobre él. En un modelo de la atmósfera, se supone que…') |
|||
| Línea 14: | Línea 14: | ||
==Presión en función de la altura== | ==Presión en función de la altura== | ||
| + | El peso de la columna de aire es proporcional a su masa. Su módulo es <math>P = mg</math>, por tanto se trata de hallar la masa de una columna de aire que se extiende desde la altura <math>z_0</math> hasta el infinito. Dado que conocemos la densidad, esta masa será igual a | ||
| + | |||
| + | <center><math>\mathrm{d}m = \rho\,\mathrm{d}V\qquad\Rightarrow\qquadm = \int_V \rho\,\mathrm{dV}</math></center> | ||
| + | |||
| + | Ahora bien, el volumen no es una sola variable, por lo que para poder calcular esta integral debemos reducirlo de forma que varíe una sola cantidad. La forma de hacerlo es muy similar al problema de la [[Cálculo_de_la_masa_de_una_esfera#Masa|masa de una esfera]]. En este caso, teniendo en cuenta que la densidad depende solo de la altura, podemos dividir la columna en capas horizontales. Cada capa será un pequeño prisma de base <math>L^2</math> y altura <math>\mathrm{d}z</math> de forma que | ||
| + | |||
| + | <center><math>\mathrm{d}V = S\,h = L^2\,\mathrm{d}z</math></center> | ||
| + | |||
| + | para cada una de estas capas la densidad es uniforme y su masa diferencial vale | ||
| + | |||
| + | <center><math>\mathrm{d}m = \rho(z)\,\mathrm{d}V = \rho_0\mathrm{e}^{-\alpha z} L^2\,\mathrm{d}z</math></center> | ||
| + | |||
| + | Llevando esto a la integral nos queda | ||
| + | |||
| + | <center><math>m = \int_{z_0}^\infty \rho_0\mathrm{e}^{-\alpha z} L^2\,\mathrm{d}z</math></center> | ||
| + | |||
| + | Este cálculo resulta en | ||
| + | |||
| + | <center><math>m(z_0) = \left.-\frac{\frac{\rho_0 L^2}{\alpha}\mathrm{e}^{-\alpha z}\right|_{z_0}^\infty = \frac{\rho_0 L^2}{\alpha}}\mathrm{e}^{-\alpha z_0}</math></center> | ||
| + | |||
| + | La presión ejercida por esta columna vale entonces | ||
| + | |||
| + | <center><math>p(z_0) = \frac{mg}{L^2}= \frac{\rho_0 g}{\alpha}\mathrm{e}^{-\alpha z_0}</math></center> | ||
| + | |||
| + | esto es, decae, como la densidad, exponencialmente con la altura. | ||
==Constante α== | ==Constante α== | ||
==Presión en La Paz== | ==Presión en La Paz== | ||
==Masa de la atmósfera== | ==Masa de la atmósfera== | ||
[[Categoría:Problemas de herramientas matemáticas (GIE)]] | [[Categoría:Problemas de herramientas matemáticas (GIE)]] | ||
Revisión de 10:04 22 oct 2011
Contenido |
1 Enunciado
La presión atmosférica en un punto se debe al peso por unidad de superficie de la columna de aire situada sobre él. En un modelo de la atmósfera, se supone que la densidad del aire disminuye con la altura como

extendiéndose la altura hasta el infinito.
- Determine el peso del aire situado por encima de un cuadrado de lado L situado a una altura z0 sobre el nivel del mar. A partir de aquí halle como varía la presión atmosférica con la altura.
- Sabiendo que al nivel del mar la presión es de 101325 Pa y la densidad del aire es de 1.225 kg/m³, calcule el valor de la constante α.
- Usando esta fórmula halle el valor de la presión atmosférica en La Paz, situada a 3650 m de altitud.
- Halle el valor aproximado de la masa de aire de la atmósfera.
En todos los pasos, razone los cálculos y justifique las aproximaciones que se hagan.
2 Presión en función de la altura
El peso de la columna de aire es proporcional a su masa. Su módulo es P = mg, por tanto se trata de hallar la masa de una columna de aire que se extiende desde la altura z0 hasta el infinito. Dado que conocemos la densidad, esta masa será igual a
Ahora bien, el volumen no es una sola variable, por lo que para poder calcular esta integral debemos reducirlo de forma que varíe una sola cantidad. La forma de hacerlo es muy similar al problema de la masa de una esfera. En este caso, teniendo en cuenta que la densidad depende solo de la altura, podemos dividir la columna en capas horizontales. Cada capa será un pequeño prisma de base L2 y altura dz de forma que
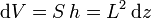
para cada una de estas capas la densidad es uniforme y su masa diferencial vale
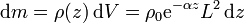
Llevando esto a la integral nos queda

Este cálculo resulta en
La presión ejercida por esta columna vale entonces
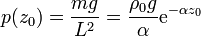
esto es, decae, como la densidad, exponencialmente con la altura.





