Ejemplo de movimiento helicoidal (GIE)
De Laplace
(Diferencias entre revisiones)
| Línea 2: | Línea 2: | ||
El movimiento de un pájaro en una corriente térmica es aproximadamente helicoidal, compuesto de un movimiento ascensional y uno de giro alrededor del eje de subida, de forma que la velocidad en cada punto de la trayectoria puede escribirse como | El movimiento de un pájaro en una corriente térmica es aproximadamente helicoidal, compuesto de un movimiento ascensional y uno de giro alrededor del eje de subida, de forma que la velocidad en cada punto de la trayectoria puede escribirse como | ||
| - | <center><math>\vec{v}=\vec{v}_0+\vec{\omega}\times\vec{r}</math></center> | + | <center><math>\vec{v}=\vec{v}_0+\vec{\omega}_0\times\vec{r}</math></center> |
siendo | siendo | ||
| - | <center><math>\vec{v}_0 = v_0\vec{k}\qquad \vec{\omega}=\ | + | <center><math>\vec{v}_0 = v_0\vec{k}\qquad \vec{\omega}_0=\omega_0 \vec{k}</math></center> |
| - | dos vectores constantes. Si la posición inicial es <math>\vec{r}_0= | + | dos vectores constantes. Si la posición inicial es <math>\vec{r}_0=A\vec{\imath}</math> |
# Determine la velocidad en cada punto expresada en la base de coordenadas cilíndricas. | # Determine la velocidad en cada punto expresada en la base de coordenadas cilíndricas. | ||
| Línea 14: | Línea 14: | ||
# Calcule la aceleración del movimiento, así como sus componentes intrínsecas en cada punto del movimiento. | # Calcule la aceleración del movimiento, así como sus componentes intrínsecas en cada punto del movimiento. | ||
# Determine el radio de curvatura de la trayectoria en cualquier instante. | # Determine el radio de curvatura de la trayectoria en cualquier instante. | ||
| + | ==Velocidad== | ||
| + | La velocidad en cada punto la obtenemos simplemente sustituyendo en la expresión indicada | ||
| + | <center><math>\vec{v}=\vec{v}_0+\vec{\omega}_0\times\vec{r}</math></center> | ||
| + | |||
| + | donde <math>\vec{r}</math> es el vector de posición del pájaro, que en coordenadas cilíndricas se expresa | ||
| + | |||
| + | <math>\vec{r}=\rho\vec{u}_\rho+z\vec{u}_z</math> | ||
| + | |||
| + | Sustituyendo nos queda | ||
| + | |||
| + | <center><math>\vec{v}=v_0\vec{k}+\omega_0\vec{k}\times\left(\rho\vec{u}_\rho+z\vec{u}_z\right)</math></center> | ||
| + | |||
| + | La base asociada a las coordenadas cilíndricas forma un ortonormal y dextrógira, por lo que cumple | ||
| + | |||
| + | <center><math>\vec{k}\times\vec{u}_\rho=\vec{u}_\varphi</math></center> | ||
| + | |||
| + | y queda la velocidad | ||
| + | |||
| + | <center><math>\vec{v}=\omega_0\rho\vec{u}_\varphi+v_0\vec{k}</math></center> | ||
| + | |||
| + | Vemos que posee una componente acimutal (correspondiente al giro) y una vertical, asociada a la ascensión. | ||
| + | |||
| + | ==Ecuaciones horarias== | ||
| + | ==Aceleración== | ||
| + | ==Radio de curvatura== | ||
[[Categoría:Problemas de cinemática de la partícula (GIE)]] | [[Categoría:Problemas de cinemática de la partícula (GIE)]] | ||
[[Categoría:Problemas de cinemática tridimensional (GIE)]] | [[Categoría:Problemas de cinemática tridimensional (GIE)]] | ||
Revisión de 15:40 12 oct 2011
Contenido |
1 Enunciado
El movimiento de un pájaro en una corriente térmica es aproximadamente helicoidal, compuesto de un movimiento ascensional y uno de giro alrededor del eje de subida, de forma que la velocidad en cada punto de la trayectoria puede escribirse como
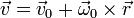
siendo
dos vectores constantes. Si la posición inicial es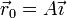 
- Determine la velocidad en cada punto expresada en la base de coordenadas cilíndricas.
- Determine las ecuaciones horarias ρ = ρ(t),
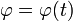y z = z(t). ¿Cuánto vale el paso de rosca de la hélice, esto es, lo que sube en el tiempo que da una vuelta alrededor del eje?
- Calcule la aceleración del movimiento, así como sus componentes intrínsecas en cada punto del movimiento.
- Determine el radio de curvatura de la trayectoria en cualquier instante.
2 Velocidad
La velocidad en cada punto la obtenemos simplemente sustituyendo en la expresión indicada
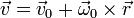
donde 
es el vector de posición del pájaro, que en coordenadas cilíndricas se expresa
Sustituyendo nos queda
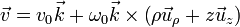
La base asociada a las coordenadas cilíndricas forma un ortonormal y dextrógira, por lo que cumple
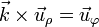
y queda la velocidad
Vemos que posee una componente acimutal (correspondiente al giro) y una vertical, asociada a la ascensión.
