Trabajo en una semicircunferencia
De Laplace
(→Solución) |
|||
| Línea 9: | Línea 9: | ||
La clave para realizar integrales definidas es leerlas al pie de la letra. En este caso, se trata de dividir una curva en trocitos. Para cada trocito, hallar el producto escalar de la fuerza por el desplazamiento y sumar todos los trocitos. | La clave para realizar integrales definidas es leerlas al pie de la letra. En este caso, se trata de dividir una curva en trocitos. Para cada trocito, hallar el producto escalar de la fuerza por el desplazamiento y sumar todos los trocitos. | ||
| - | En este caso nuestra curva es una semicircunferencia que va desde un punto que podemos llamar “polo norte” <math>\vec{r} | + | En este caso nuestra curva es una semicircunferencia que va desde un punto que podemos llamar “polo norte” <math>\vec{r}_A=+R\vec{k}</math> hasta otro que sería el “polo sur” <math>\vec{r}_B = -R\vec{k}</math> a lo largo de una curva que en la superficie terrestre sería un meridiano. |
Para identificar los puntos de este meridiano, definimos un ángulo <math>\theta</math> que varía desde 0 en el polo norte hasta π en el polo sur. | Para identificar los puntos de este meridiano, definimos un ángulo <math>\theta</math> que varía desde 0 en el polo norte hasta π en el polo sur. | ||
| Línea 21: | Línea 21: | ||
Cuando multiplicamos este desplazamiento por la fuerza que actúa sobre la partícula en ese punto obtenemos | Cuando multiplicamos este desplazamiento por la fuerza que actúa sobre la partícula en ese punto obtenemos | ||
| - | <center><math>\vec{F}\cdot\mathrm{d}\vec{r} = |\vec{F}||\mathrm{d} | + | <center><math>\vec{F}\cdot\mathrm{d}\vec{r} = |\vec{F}||\mathrm{d}\vec{r}|\cos(\alpha)</math></center> |
El ángulo <math>\alpha</math> que forma la fuerza con el desplazamiento no es igual al ángulo <math>\theta</math>, sino a su complementario | El ángulo <math>\alpha</math> que forma la fuerza con el desplazamiento no es igual al ángulo <math>\theta</math>, sino a su complementario | ||
| Línea 31: | Línea 31: | ||
<center><math>\vec{F}\cdot\mathrm{d}\vec{r} = -mgR\,\mathrm{sen}(\theta)\,\mathrm{d}\theta</math></center> | <center><math>\vec{F}\cdot\mathrm{d}\vec{r} = -mgR\,\mathrm{sen}(\theta)\,\mathrm{d}\theta</math></center> | ||
| + | Se trata entonces de hallar la integral | ||
| + | |||
| + | <center><math>W = \int_0^\pi mgR \mathrm{sen}(\theta)\,\mathrm{d}\theta</math></center> | ||
| + | |||
| + | Este es el único punto en el que realmente hay que calcular una primitiva, que en este caso es inmediata | ||
| + | |||
| + | <center><math>W = \left.-mgr\cos(\theta)\right|_0^\pi = 2mgR</math></center> | ||
[[Categoría:Problemas de herramientas matemáticas (GIE)]] | [[Categoría:Problemas de herramientas matemáticas (GIE)]] | ||
Revisión de 10:51 8 oct 2011
1 Enunciado
Una partícula se encuentra sometida a su peso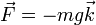 
. Halle el trabajo realizado por esta fuerza
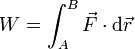
cuando la partícula pasa de 
a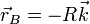 
moviéndose sobre una semicircunferencia vertical de radio R con centro el origen de coordenadas.
2 Solución
La clave para realizar integrales definidas es leerlas al pie de la letra. En este caso, se trata de dividir una curva en trocitos. Para cada trocito, hallar el producto escalar de la fuerza por el desplazamiento y sumar todos los trocitos.
En este caso nuestra curva es una semicircunferencia que va desde un punto que podemos llamar “polo norte”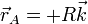 
hasta otro que sería el “polo sur” 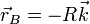a lo largo de una curva que en la superficie terrestre sería un meridiano.
Para identificar los puntos de este meridiano, definimos un ángulo θ que varía desde 0 en el polo norte hasta π en el polo sur.
Cuando variamos θ en una cantidad diferencial dθ realizamos un desplazamiento cuya longitud es igual al radio por el ángulo
con dirección tangente al meridiano y sentido hacia el sur.
Cuando multiplicamos este desplazamiento por la fuerza que actúa sobre la partícula en ese punto obtenemos
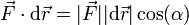
El ángulo α que forma la fuerza con el desplazamiento no es igual al ángulo θ, sino a su complementario
y por tanto el producto escalar vale
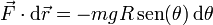
Se trata entonces de hallar la integral
Este es el único punto en el que realmente hay que calcular una primitiva, que en este caso es inmediata
