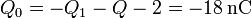Sistema de dos bloques conductores
De Laplace
(→Estado de equilibrio inicial) |
(→Estado de equilibrio inicial) |
||
| Línea 28: | Línea 28: | ||
En el estado inicial conocemos la carga de los dos conductores | En el estado inicial conocemos la carga de los dos conductores | ||
| - | <center><math>Q_1 = 18\,\mathrm{nC}\qquad Q_2 = 0\,\ | + | <center><math>Q_1 = 18\,\mathrm{nC}\qquad Q_2 = 0\,\mathrm{nC}</math></center> |
y se trata de hallar las respectivas tensiones. Si expresamos la carga en picoculombios, el voltaje en voltios y la capacidad en picofaradios, nos queda el sistema | y se trata de hallar las respectivas tensiones. Si expresamos la carga en picoculombios, el voltaje en voltios y la capacidad en picofaradios, nos queda el sistema | ||
Revisión de 23:42 1 sep 2011
Contenido |
1 Enunciado
2 Coeficientes de capacidad
La forma más sencilla de calcular los coeficientes de capacidad e inducción es mediante el circuito equivalente.
El circuito equivalente está formado por dos nodos y tres condensadores. Los nodos representan a los dos bloques. Los condensadores son uno de capacidad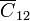 
entre ambos nodos y que representa las líneas de campo que van de un bloque a otro, y dos condensadores 
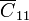y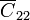 
, que representan las líneas de campo que conectan cada bloque con la caja exterior.
Para hallar los valores de las capacidades, despreciamos los efectos de borde, por lo que se pueden tratar como una asociación de condensadores planos. Si tomamos como unidad un condensador cuya superficie sea un rectángulo de 25 mm×50 mm y distancia entre placas 1 mm, con capacidad
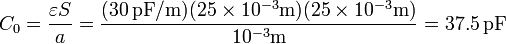
Entonces, el condensador que forman los dos bloques tiene el doble de esta área y por tanto el doble de capacidad
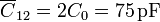
Los que forma cada bloque con la caja exterior equivale a 6 veces el condensador unidad (2 veces en la cara cuadrada y las 4 caras laterales)
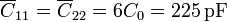
Una vez que tenemos las capacidades es inmediato hallar los coeficientes de capacidad
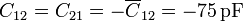
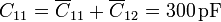
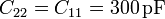
o, en forma matricial
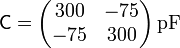
3 Estado de equilibrio inicial
En el estado inicial conocemos la carga de los dos conductores
y se trata de hallar las respectivas tensiones. Si expresamos la carga en picoculombios, el voltaje en voltios y la capacidad en picofaradios, nos queda el sistema
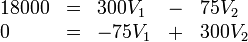
Despejando en la segunda y sustituyendo en la primera
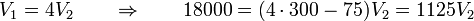
y de aquí
La energía almacenada en el sistema es igual a
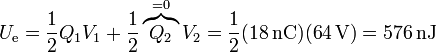
La carga almacenada en las paredes de la caja exterior, por el teorema de Faraday, es igual a la carga contenida en su interior, cambiada de signo
