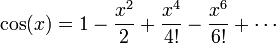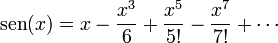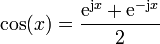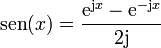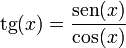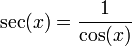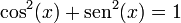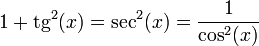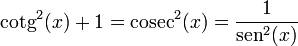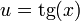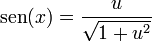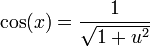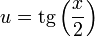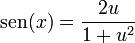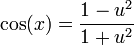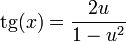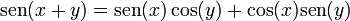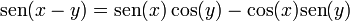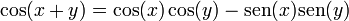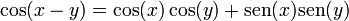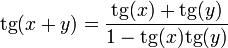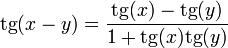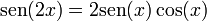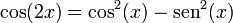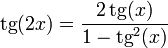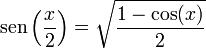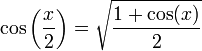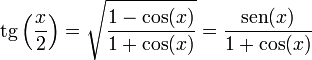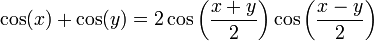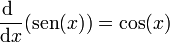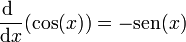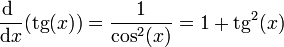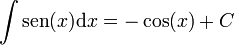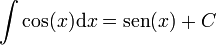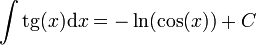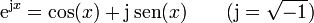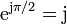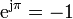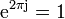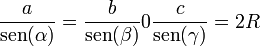Entrar Página Discusión Historial Go to the site toolbox

Tabla de fórmulas de trigonometría

De Laplace

(Diferencias entre revisiones)
(→Fórmula de Euler)
(→Teorema del seno)
Línea 197: Línea 197:
:<math>\mathrm{e}^{2\pi\mathrm{j}} = 1\,</math>
:<math>\mathrm{e}^{2\pi\mathrm{j}} = 1\,</math>
-
==Teorema del seno==
+
==Teoremas del seno y del coseno==
 +
===Teorema del seno===
 +
:<math>\frac{a}{\mathrm{sen}(\alpha)}=\frac{b}{\mathrm{sen}(\beta)}0\frac{c}{\mathrm{sen}(\gamma)}=2R</math>
 +
 
 +
(R: radio de la circunferencia circunscrita)
 +
 
==Teorema del coseno==
==Teorema del coseno==

Revisión de 19:32 29 ago 2011

Contenido

1 Definiciones

1.1 Geométrica

\cos(x)=\frac{a}{r}\qquad\mathrm{sen}(x) = \frac{b}{r}

1.2 Analítica

El argumento x debe estar expresado en radianes

\cos(x) = 1 -\frac{x^2}{2}+\frac{x^4}{4!}-\frac{x^6}{6!}+\cdots
\mathrm{sen}(x) = x -\frac{x^3}{6}+\frac{x^5}{5!}-\frac{x^7}{7!}+\cdots

1.3 Exponenciales complejas

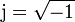(\mathrm{j}=\sqrt{-1})

\cos(x) = \frac{\mathrm{e}^{\mathrm{j}x}+\mathrm{e}^{-\mathrm{j}x}}{2}
\mathrm{sen}(x) = \frac{\mathrm{e}^{\mathrm{j}x}-\mathrm{e}^{-\mathrm{j}x}}{2\mathrm{j}}

1.4 Funciones adicionales

\mathrm{tg}(x) = \frac{\mathrm{sen}(x)}{\cos(x)}
\mathrm{cotg}(x) = \frac{\cos(x)}{\mathrm{sen}(x)} = \frac{1}{\mathrm{tg}(x)}
\mathrm{sec}(x) = \frac{1}{\cos(x)}
\mathrm{cosec}(x) = \frac{1}{\mathrm{sen}(x)}

2 Relaciones entre funciones

2.1 Identidades básicas

\cos^2(x) + \mathrm{sen}^2(x) = 1\,
1 + \mathrm{tg}^2(x) = \mathrm{sec}^2(x)=\frac{1}{\cos^2(x)}\,
\mathrm{cotg}^2(x) +1= \mathrm{cosec}^2(x)=\frac{1}{\mathrm{sen}^2(x)}\,

2.2 En función de la tangente

u = \mathrm{tg}(x)\,
\mathrm{sen}(x) = \frac{u}{\sqrt{1+u^2}}
\cos(x) = \frac{1}{\sqrt{1+u^2}}

2.3 En función de la tangente del ángulo mitad

u = \mathrm{tg}\left(\frac{x}{2}\right)\,
\mathrm{sen}(x) = \frac{2u}{1+u^2}
\cos(x) = \frac{1-u^2}{1+u^2}
\mathrm{tg}(x) = \frac{2u}{1-u^2}

3 Tabla de valores particulares

° rad sen cos tg
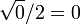
0\, 0\, \sqrt{0}/2 = 0 1\, 0\,
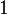
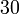
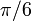
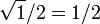
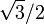
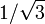
30\, \pi/6\, \sqrt{1}/2 = 1/2\, \sqrt{3}/2 1/\sqrt{3}
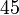
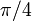
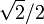
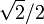
45\, \pi/4\, \sqrt{2}/2 \sqrt{2}/2 1\,
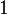
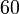
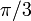
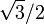
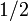
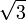
60\, \pi/3\, \sqrt{3}/2 1/2\, \sqrt{3}
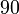
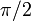
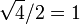
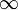
90\, \pi/2\, \sqrt{4}/2=1 0\, \infty
Ángulo complementario
\mathrm{sen}\left(\frac{\pi}{2}-x\right)=\cos(x)\qquad \cos\left(\frac{\pi}{2}-x\right)=\mathrm{sen}(x)
Ángulo suplementario
\mathrm{sen}\left(\pi-x\right)=\mathrm{sen}(x)\qquad \cos\left(\pi-x\right)=-\cos(x)
Giro de un cuadrante
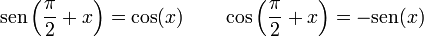
\mathrm{sen}\left(\frac{\pi}{2}+x\right)=\cos(x)\qquad \cos\left(\frac{\pi}{2}+x\right)=-\mathrm{sen}(x)
Giro de dos cuadrantes
\mathrm{sen}\left(\pi+x\right)=-\mathrm{sen}(x)\qquad \cos\left(\pi+x\right)=-\cos(x)
Cambio de signo
\mathrm{sen}\left(-x\right)=-\mathrm{sen}(x)\qquad \cos\left(-x\right)=\cos(x)

4 Suma y diferencia de ángulos

Seno
\mathrm{sen}(x+y)=\mathrm{sen}(x)\cos(y)+\cos(x)\mathrm{sen}(y)\,
\mathrm{sen}(x-y)=\mathrm{sen}(x)\cos(y)-\cos(x)\mathrm{sen}(y)\,
Coseno
\cos(x+y)=\cos(x)\cos(y)-\mathrm{sen}(x)\mathrm{sen}(y)\,
\cos(x-y)=\cos(x)\cos(y)+\mathrm{sen}(x)\mathrm{sen}(y)\,
Tangente
\mathrm{tg}(x+y)=\frac{\mathrm{tg}(x)+\mathrm{tg}(y)}{1-\mathrm{tg}(x)\mathrm{tg}(y)}
\mathrm{tg}(x-y)=\frac{\mathrm{tg}(x)-\mathrm{tg}(y)}{1+\mathrm{tg}(x)\mathrm{tg}(y)}

5 Ángulo doble y ángulo mitad

5.1 Ángulo doble

Seno
\mathrm{sen}(2x)=2\mathrm{sen}(x)\cos(x)\,
Coseno
\cos(2x)=\cos^2(x)-\mathrm{sen}^2(x)\,
Tangente
\mathrm{tg}(2x)=\frac{2\,\mathrm{tg}(x)}{1-\mathrm{tg}^2(x)}

5.2 Ángulo mitad

Seno
\mathrm{sen}\left(\frac{x}{2}\right)=\sqrt{\frac{1-\cos(x)}{2}}
Coseno
\cos\left(\frac{x}{2}\right)=\sqrt{\frac{1+\cos(x)}{2}}
Tangente
\mathrm{tg}\left(\frac{x}{2}\right)=\sqrt{\frac{1-\cos(x)}{1+\cos(x)}}=\frac{\mathrm{sen}(x)}{1+\cos(x)}

6 Sumas en productos

\mathrm{sen}(x)+\mathrm{sen}(y) = 2\,\mathrm{sen}\left(\frac{x+y}{2}\right)\cos\left(\frac{x-y}{2}\right)
\mathrm{sen}(x)-\mathrm{sen}(y) = 2\,\mathrm{sen}\left(\frac{x-y}{2}\right)\cos\left(\frac{x+y}{2}\right)
\cos(x)+\cos(y) = 2\cos\left(\frac{x+y}{2}\right)\cos\left(\frac{x-y}{2}\right)
\cos(x)-\cos(y) = -2\,\mathrm{sen}\left(\frac{x+y}{2}\right)\mathrm{sen}\left(\frac{x-y}{2}\right)

7 Derivadas y primitivas

El argumento debe estar obligatoriamente en radianes

7.1 Derivadas

\frac{\mathrm{d}\ }{\mathrm{d}x}(\mathrm{sen}(x)) = \cos(x)
\frac{\mathrm{d}\ }{\mathrm{d}x}(\cos(x)) = -\mathrm{sen}(x)
\frac{\mathrm{d}\ }{\mathrm{d}x}(\mathrm{tg}(x)) = \frac{1}{\cos^2(x)}=1+\mathrm{tg}^2(x)

7.2 Primitivas

\int \mathrm{sen}(x)\mathrm{d}x = -\cos(x)+C
\int \cos(x)\mathrm{d}x = \mathrm{sen}(x)+C
\int \mathrm{tg}(x)\mathrm{d}x = -\ln(\cos(x))+C

8 Fórmula de Euler

Fórmula general
\mathrm{e}^{\mathrm{j}x}=\cos(x)+\mathrm{j}\,\mathrm{sen}(x)\qquad (\mathrm{j}=\sqrt{-1})
Casos particulares
\mathrm{e}^{\mathrm{j}\pi/2} = \mathrm{j}\,
\mathrm{e}^{\mathrm{j}\pi} = -1\,
\mathrm{e}^{2\pi\mathrm{j}} = 1\,

9 Teoremas del seno y del coseno

9.1 Teorema del seno

\frac{a}{\mathrm{sen}(\alpha)}=\frac{b}{\mathrm{sen}(\beta)}0\frac{c}{\mathrm{sen}(\gamma)}=2R

(R: radio de la circunferencia circunscrita)

10 Teorema del coseno

Obtenido de "http://tesla.us.es/wiki/index.php/Tabla_de_f%C3%B3rmulas_de_trigonometr%C3%ADa"

Herramientas:

Herramientas personales
TOOLBOX
LANGUAGES
licencia de Creative Commons
 Aviso legal - Acerca de Laplace