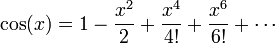Tabla de fórmulas de trigonometría
De Laplace
(Diferencias entre revisiones)
(→Geométrica) |
(→Definiciones) |
||
| Línea 2: | Línea 2: | ||
===Geométrica=== | ===Geométrica=== | ||
| - | + | :<math>\cos(x)=\frac{a}{r}\qquad\mathrm{sen}(x) = \frac{b}{r}</math> | |
===Analítica=== | ===Analítica=== | ||
| + | El argumento <math>x</math> debe estar expresado en radianes | ||
| + | |||
| + | :<math>\cos(x) = 1 -\frac{x^2}{2}+\frac{x^4}{4!}+\frac{x^6}{6!}+\cdots</math> | ||
| + | |||
| + | :<math>\cos(x) = 1 -\frac{x^2}{2}+\frac{x^4}{4!}+\frac{x^6}{6!}+\cdots</math> | ||
| + | |||
===Exponenciales complejas=== | ===Exponenciales complejas=== | ||
===Funciones adicionales=== | ===Funciones adicionales=== | ||
| + | |||
==Relaciones entre funciones== | ==Relaciones entre funciones== | ||
===En función del seno=== | ===En función del seno=== | ||
Revisión de 10:14 28 ago 2011
Contenido |
1 Definiciones
1.1 Geométrica
1.2 Analítica
El argumento x debe estar expresado en radianes