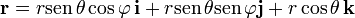Bases vectoriales
De Laplace
(Diferencias entre revisiones)
(→Introducción) |
(→Introducción) |
||
| Línea 3: | Línea 3: | ||
La definición de sistemas de coordenadas está muy bien, y es muy útil, pero, por desgracia, no es suficiente. Dado que vamos a hablar de forma insistente de magnitudes vectoriales, vamos a necesitar expresar vectores en diferentes sistemas de coordenadas. Para ello necesitamos definir bases vectoriales, para poder escribir los vectores en términos de sus componentes. Por supuesto, una posibilidad sería definir una base de una vez por todas, por ejemplo <math>\{\mathbf{i}, \mathbf{j}, \mathbf{k}\}\,</math>, y expresar todos los vectores siempre en dicha base. Pero, aunque parece lo más cómodo, no es lo más sencillo. O, mejor dicho, no es esta base la que da una expresión más sencilla para los distintos vectores. Por ejemplo, El vector de posición en esféricas, empleando la base <math>\{\mathbf{i}, \mathbf{j}, \mathbf{k}\}\,</math> se escribe | La definición de sistemas de coordenadas está muy bien, y es muy útil, pero, por desgracia, no es suficiente. Dado que vamos a hablar de forma insistente de magnitudes vectoriales, vamos a necesitar expresar vectores en diferentes sistemas de coordenadas. Para ello necesitamos definir bases vectoriales, para poder escribir los vectores en términos de sus componentes. Por supuesto, una posibilidad sería definir una base de una vez por todas, por ejemplo <math>\{\mathbf{i}, \mathbf{j}, \mathbf{k}\}\,</math>, y expresar todos los vectores siempre en dicha base. Pero, aunque parece lo más cómodo, no es lo más sencillo. O, mejor dicho, no es esta base la que da una expresión más sencilla para los distintos vectores. Por ejemplo, El vector de posición en esféricas, empleando la base <math>\{\mathbf{i}, \mathbf{j}, \mathbf{k}\}\,</math> se escribe | ||
| - | <math>\mathbf{r} = r\mathrm{sen}\,\theta\cos\varphi\,\mathbf{i} + r\mathrm{sen}\,\theta\mathrm{sen}\,\varphi \mathbf{j} + r \cos\theta\,\mathbf{k}</math> | + | <center><math>\mathbf{r} = r\mathrm{sen}\,\theta\cos\varphi\,\mathbf{i} + r\mathrm{sen}\,\theta\mathrm{sen}\,\varphi \mathbf{j} + r \cos\theta\,\mathbf{k}</math></center> |
==Artículo siguiente== | ==Artículo siguiente== | ||
Revisión de 16:58 20 nov 2007
1 Introducción
La definición de sistemas de coordenadas está muy bien, y es muy útil, pero, por desgracia, no es suficiente. Dado que vamos a hablar de forma insistente de magnitudes vectoriales, vamos a necesitar expresar vectores en diferentes sistemas de coordenadas. Para ello necesitamos definir bases vectoriales, para poder escribir los vectores en términos de sus componentes. Por supuesto, una posibilidad sería definir una base de una vez por todas, por ejemplo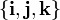 
, y expresar todos los vectores siempre en dicha base. Pero, aunque parece lo más cómodo, no es lo más sencillo. O, mejor dicho, no es esta base la que da una expresión más sencilla para los distintos vectores. Por ejemplo, El vector de posición en esféricas, empleando la base 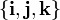se escribe
