Energía electromagnética en una onda viajera
De Laplace
(Diferencias entre revisiones)
(Página creada con '==Enunciado== Una onda plana monocromática en una región libre de fuentes posee el campo eléctrico <center><math>\mathbf{E}=E_0\cos(\omega t - k z)\mathbf{u}_x</math></cente…') |
|||
| Línea 16: | Línea 16: | ||
==Campo magnético== | ==Campo magnético== | ||
| - | Si | + | Si hallamos las fuentes vectoriales del campo eléctrico obtenemos |
| + | |||
| + | <center><math>\nabla\times\mathbf{E}=\left|\begin{matrix} \mathbf{u}_x & \mathbf{u}_y & \mathbf{u}_z \\ && \\ 0 & 0 & \displaystyle\frac{\partial }{\partial z} \\ && \\ E(z,t) & 0 & 0\end{matrix}\right| = \frac{\partial E}{\partial z}\mathbf{u}_y = k E_0\mathrm{sen}(\omega t - k z)\mathbf{u}_y</math></center> | ||
| + | |||
| + | De acuerdo con la ley de Faraday, esto debe ser igual a la derivada temporal del campo magnético, cambiada de signo. | ||
| + | |||
| + | <center><math>-\frac{\partial\mathbf{B}}{\partial t} = k E_0\mathrm{sen}(\omega t - k z)\mathbf{u}_y\qquad\Rightarrow\qquad \mathbf{B}=ºfrac{k}{\omega}\cos(\omega t - k x)\mathbf{u}_y</math></center> | ||
==Densidades de energía== | ==Densidades de energía== | ||
==Promedio de la densidad de energía== | ==Promedio de la densidad de energía== | ||
Revisión de 20:58 1 jun 2011
Contenido |
1 Enunciado
Una onda plana monocromática en una región libre de fuentes posee el campo eléctrico
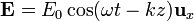
- Determine el valor del campo magnético en todos los puntos del espacio.
- Calcule las densidades de energía eléctrica y magnética en todos los puntos del espacio.
- Halle el promedio temporal de las densidades de energía, definido como
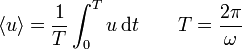
- Calcule el vector de Poynting en cada instante
- Halle el promedio temporal del vector de Poynting
2 Campo magnético
Si hallamos las fuentes vectoriales del campo eléctrico obtenemos
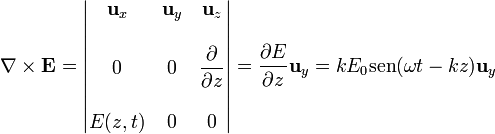
De acuerdo con la ley de Faraday, esto debe ser igual a la derivada temporal del campo magnético, cambiada de signo.






