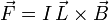Campo magnético FII GIA
De Laplace
(→Líneas de campo magnético) |
(→Fuerza y par ejercidos por un campo magnético) |
||
| Línea 2: | Línea 2: | ||
== Fuerza y par ejercidos por un campo magnético == | == Fuerza y par ejercidos por un campo magnético == | ||
| + | |||
| + | El campo magnético ejerce fuerzas sobre cargas en movimiento. Estas pueden ser cargas libres o estar incluidas en una corriente que circule por un cable. | ||
=== Fuerza sobre una carga en movimiento === | === Fuerza sobre una carga en movimiento === | ||
| + | |||
| + | Dada una carga de valor <math>q </math>, que se mueve con velocidad <math>\vec{v} </math> en el seno de un campo magnético <math>\vec{B} </math> la fuerza que el campo magnético ejerce sobre la carga es | ||
| + | <center> | ||
| + | <math> | ||
| + | \vec{F} = q\vec{v}\times\vec{B} | ||
| + | </math> | ||
| + | </center> | ||
| + | Esta fuerza tiene las siguientes propiedades | ||
| + | #La fuerza es perpendicular tanto a <math>\vec{v} </math> como a <math>\vec{B} </math> | ||
| + | #La fuerza no realiza trabajo sobre la carga, por lo que no varía su energía cinética. Por tanto, el módulo de su velocidad es constante, aunque no así su dirección. | ||
| + | ##Si una carga penetra en una región de campo uniforme con un velocidad perpendicular al campo se mueve describiendo una circunferencia en un plano perpendicular a las líneas de campo. | ||
| + | #El módulo de la fuerza es proporcional al módulo de la velocidad, al módulo del campo y al seno del ángulo que forman. | ||
| + | |||
| + | Si en la región en que se mueve la carga hay a la vez un campo eléctrico y un campo magnético la fuerza total sobre la carga es la suma de la fuerza eléctrica y la magnética. | ||
| + | <center> | ||
| + | <math> | ||
| + | \vec{F} = q(\vec{E}+\vec{v}\times\vec{B}) | ||
| + | </math> | ||
| + | </center> | ||
| + | Esta fuerza recibe el nombre de Fuerza de Lorentz. | ||
| + | |||
| + | === Fuerza sobre una corriente === | ||
| + | |||
| + | ==== Hilo recto==== | ||
| + | Supongamos un hilo recto de longitud <math>L </math> por el que circula una corriente <math>I </math>. Si el hilo está en el seno de un campo magnético uniforme, este campo ejerce una fuerza sobre cada carga que se mueve en el hilo. La fuerza total es la suma de las fuerzas sobre todas las cargas que se mueven en el hilo. Esta expresión es | ||
| + | <center> | ||
| + | <math> | ||
| + | \vec{F} = I\,\vec{L}\times\vec{B} | ||
| + | </math> | ||
| + | </center> | ||
| + | |||
=== Fuerza y par sobre una espira === | === Fuerza y par sobre una espira === | ||
Revisión de 13:07 5 abr 2011
Contenido |
1 Introducción
2 Fuerza y par ejercidos por un campo magnético
El campo magnético ejerce fuerzas sobre cargas en movimiento. Estas pueden ser cargas libres o estar incluidas en una corriente que circule por un cable.
2.1 Fuerza sobre una carga en movimiento
Dada una carga de valor q, que se mueve con velocidad 
en el seno de un campo magnético 
la fuerza que el campo magnético ejerce sobre la carga es
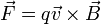
Esta fuerza tiene las siguientes propiedades
- La fuerza es perpendicular tanto a como a
- La fuerza no realiza trabajo sobre la carga, por lo que no varía su energía cinética. Por tanto, el módulo de su velocidad es constante, aunque no así su dirección.
- Si una carga penetra en una región de campo uniforme con un velocidad perpendicular al campo se mueve describiendo una circunferencia en un plano perpendicular a las líneas de campo.
- El módulo de la fuerza es proporcional al módulo de la velocidad, al módulo del campo y al seno del ángulo que forman.
Si en la región en que se mueve la carga hay a la vez un campo eléctrico y un campo magnético la fuerza total sobre la carga es la suma de la fuerza eléctrica y la magnética.
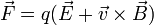
Esta fuerza recibe el nombre de Fuerza de Lorentz.
2.2 Fuerza sobre una corriente
2.2.1 Hilo recto
Supongamos un hilo recto de longitud L por el que circula una corriente I. Si el hilo está en el seno de un campo magnético uniforme, este campo ejerce una fuerza sobre cada carga que se mueve en el hilo. La fuerza total es la suma de las fuerzas sobre todas las cargas que se mueven en el hilo. Esta expresión es
