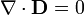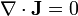Pulso gaussiano de tensión
De Laplace
(Página creada con '==Enunciado== Se tiene un condensador con pérdidas formado por dos placas cuadradas de lado <math>L = 20\,\mathrm{cm}</math>, situadas paralelamente a una distancia <math>a = 5…') |
|||
| Línea 19: | Línea 19: | ||
<center><math>\int_{-\infty}^{\infty}\mathrm{e}^{-x^2}\mathrm{d}x = \sqrt{\pi}</math></center> | <center><math>\int_{-\infty}^{\infty}\mathrm{e}^{-x^2}\mathrm{d}x = \sqrt{\pi}</math></center> | ||
| + | ==Campo y densidad de corriente== | ||
| + | En principio tenemos un sistema complicado de ecuaciones diferenciales y relaciones constitutivas | ||
| + | |||
| + | <center><math>\nabla\times\mathbf{E}=\mathbf{0}</math>{{qquad}}{{qquad}}<math>\nabla\cdot\mathbf{D}=\rho_l</math>{{qquad}}{{qquad}}<math>\nabla\cdot\mathbf{J}=-\frac{\partial \rho_l}{\partial t}</math></center> | ||
| + | |||
| + | <center><math>\mathbf{D}=\varepsilon \mathbf{E}\qquad\mathbf{J}=\sigma\mathbf{E}</math></center> | ||
| + | |||
| + | Sin embargo, por tratarse de un medio homogéneo, se cumple que, si no existe la densidad de carga libre es nula en el instante inicial, también lo es en cualquier otro instante | ||
| + | |||
| + | <center><math>\rho_l=0\,</math></center> | ||
| + | |||
| + | Por tanto, las ecuaciones se reducen a | ||
| + | |||
| + | <center><math>\nabla\times\mathbf{E}=\mathbf{0}</math>{{qquad}}{{qquad}}<math>\nabla\cdot\mathbf{D}=0</math>{{qquad}}{{qquad}}<math>\nabla\cdot\mathbf{J}=0</math></center> | ||
| + | |||
| + | ==Carga e intensidad de corriente== | ||
| + | ==Balance energético== | ||
| + | ==Energía total disipada== | ||
[[Categoría:Problemas de corriente eléctrica]] | [[Categoría:Problemas de corriente eléctrica]] | ||
Revisión de 17:59 28 feb 2011
Contenido |
1 Enunciado
Se tiene un condensador con pérdidas formado por dos placas cuadradas de lado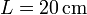 
, situadas paralelamente a una distancia 
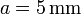. Entre ellas se encuentra un material de permitividad relativa 
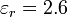y conductividad 
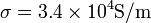. Una placa se encuentra permanentemente a tierra, mientras que la otra experimenta un pulso de tensión de forma gaussiana
con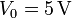 
y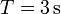 
.
Para cualquier instante de tiempo, calcule
- la distribución de campo eléctrico y de corriente entre las placas. Desprecie los efectos de borde.
- la carga en cada una de las placas y la corriente que llega a cada una.
- la energía electrostática almacenada, la potencia disipada en el medio, y la potencia desarrollada por el generador.
- Calcule igualmente la energía total disipada a lo largo del tiempo, así como el trabajo total realizado por el generador.
Halle el valor numérico de los resultado sélo para el último apartado.
Dato:
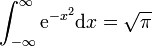
2 Campo y densidad de corriente
En principio tenemos un sistema complicado de ecuaciones diferenciales y relaciones constitutivas
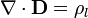
Sin embargo, por tratarse de un medio homogéneo, se cumple que, si no existe la densidad de carga libre es nula en el instante inicial, también lo es en cualquier otro instante
Por tanto, las ecuaciones se reducen a
