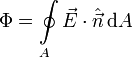Campo eléctrico FII GIA
De Laplace
(→Ley de Gauss) |
(→Ley de Gauss) |
||
| Línea 5: | Línea 5: | ||
=== Flujo eléctrico === | === Flujo eléctrico === | ||
| + | ==== Campo uniforme y superficie perpendicular ==== | ||
Consideremos una región del espacio donde hay definido un campo eléctrico uniforme. Si dibujamos una superficie que sea perpendicular al campo eléctrico, podemos imaginar las líneas de campo eléctrico atravesando esta superficie. Este es el '''flujo del campo eléctrico'''. Es similar al flujo de agua a través de la sección de una tubería. | Consideremos una región del espacio donde hay definido un campo eléctrico uniforme. Si dibujamos una superficie que sea perpendicular al campo eléctrico, podemos imaginar las líneas de campo eléctrico atravesando esta superficie. Este es el '''flujo del campo eléctrico'''. Es similar al flujo de agua a través de la sección de una tubería. | ||
Definimos el flujo eléctrico a través de una superficie perpendicular al campo como | Definimos el flujo eléctrico a través de una superficie perpendicular al campo como | ||
| Línea 14: | Línea 15: | ||
siendo <math>A </math> el área de la superficie. El flujo es proporcional al número de líneas de campo eléctrico que atraviesan la superficie. | siendo <math>A </math> el área de la superficie. El flujo es proporcional al número de líneas de campo eléctrico que atraviesan la superficie. | ||
| - | [[Imagen:FII_GIA_flujo_superficie_inclinada.jpg| | + | ==== Campo uniforme y superficie inclinada ==== |
| + | [[Imagen:FII_GIA_flujo_superficie_inclinada.jpg|250px|right]] | ||
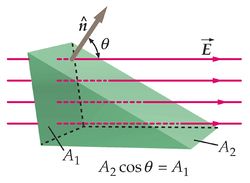
Consideramos ahora el caso en el que la superficie no es normal al campo eléctrico. | Consideramos ahora el caso en el que la superficie no es normal al campo eléctrico. | ||
La imagen de la derecha muestra dos superficies <math>A_1 </math> y <math>A_2 </math>. La primera de ellas es perpendicular al campo, mientras que la segunda está inclinada. Esta inclinación puede medirse como el ángulo <math>\theta </math> que forma el vector normal a la superficie, <math>\hat{\vec{n}} </math> con el campo. | La imagen de la derecha muestra dos superficies <math>A_1 </math> y <math>A_2 </math>. La primera de ellas es perpendicular al campo, mientras que la segunda está inclinada. Esta inclinación puede medirse como el ángulo <math>\theta </math> que forma el vector normal a la superficie, <math>\hat{\vec{n}} </math> con el campo. | ||
| Línea 25: | Línea 27: | ||
</center> | </center> | ||
| + | [[Imagen:F2_GIA_area_superficie_inclinada.png|left]] | ||
| + | Podemos relacionar el área de las dos superficies usando la figura de la izquierda. Vemos que | ||
| + | <center> | ||
| + | <math> | ||
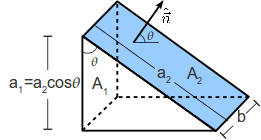
| + | A_1 = b\,a_1 = b\,a_2\cos\theta = A_2\cos\theta | ||
| + | </math> | ||
| + | </center> | ||
| + | |||
| + | Por tanto, el flujo a través de la superficie inclinada es | ||
| + | <center> | ||
| + | <math> | ||
| + | \Phi_2 = E\,A_1 = E\,A_2\cos\theta | ||
| + | </math> | ||
| + | </center> | ||
| + | Esto se puede expresar en forma vectorial usando el vector unitario normal a la superficie. Para una superficie general, tenemos | ||
| + | <center> | ||
| + | <math> | ||
| + | \Phi = E\,A\cos\theta = \vec{E}\cdot\hat{\vec{n}}\,A | ||
| + | </math> | ||
| + | </center> | ||
| + | |||
| + | ==== Campo no uniforme y superficie arbitraria ==== | ||
| + | [[Imagen:F2_GIA_flujo_general.jpg|250px|right]] | ||
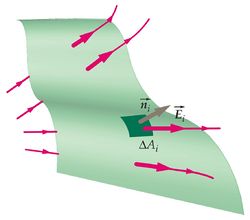
| + | En el caso más general el campo eléctrico varía de un punto a otro de la superficie y ésta puede tener cualquier forma. Recurrimos entonces al cálculodiferencial. Dividimos la superficie en elementos de área, cada elemento con un vector normal <math>\hat{\vec{n}} </math> y área <math>\mathrm{d}A </math>. El flujo a través de cada elemento es | ||
| + | <center> | ||
| + | <math> | ||
| + | \mathrm{d}\Phi = \vec{E}\cdot\hat{\vec{n}}\,\mathrm{d}A | ||
| + | </math> | ||
| + | </center> | ||
| + | El flujo a través de toda la superficie es la suma de los flujos a través de cada elemento de área que podemos tomar en ella. Es decir | ||
| + | <center> | ||
| + | <math> | ||
| + | \Phi = \int\limits_A \vec{E}\cdot\hat{\vec{n}}\,\mathrm{d}A | ||
| + | </math> | ||
| + | </center> | ||
| + | |||
| + | ==== Superficie cerrada ==== | ||
| + | Una superficie cerrada divide al espacio en dos partes, el interior y el exterior. Por convenio, el vector normal a una superficie cerrada se considera positivo cuando apunta hacia el exterior de la superficie. Al calcular el flujo del campo a través de una superficie cerrada se coloca un pequeño círculo en el signo integral | ||
| + | <center> | ||
| + | <math> | ||
| + | \Phi = \oint\limits_A \vec{E}\cdot\hat{\vec{n}}\,\mathrm{d}A | ||
| + | </math> | ||
| + | </center> | ||
Revisión de 13:48 16 feb 2011
Contenido |
1 Ley de Gauss
La ley de Gauss es una de las cuatro leyes de Maxwell, y como tal una de las leyes básicas del Electromagnetismo. Relaciona el flujo de campo eléctrico a través de una superficie cerrada con la carga neta encerrada en esa superficie. Está basada en las propiedades de simetría espacial del campo eléctrico.
1.1 Flujo eléctrico
1.1.1 Campo uniforme y superficie perpendicular
Consideremos una región del espacio donde hay definido un campo eléctrico uniforme. Si dibujamos una superficie que sea perpendicular al campo eléctrico, podemos imaginar las líneas de campo eléctrico atravesando esta superficie. Este es el flujo del campo eléctrico. Es similar al flujo de agua a través de la sección de una tubería. Definimos el flujo eléctrico a través de una superficie perpendicular al campo como
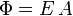
siendo A el área de la superficie. El flujo es proporcional al número de líneas de campo eléctrico que atraviesan la superficie.
1.1.2 Campo uniforme y superficie inclinada
Consideramos ahora el caso en el que la superficie no es normal al campo eléctrico.
La imagen de la derecha muestra dos superficies A1 y A2. La primera de ellas es perpendicular al campo, mientras que la segunda está inclinada. Esta inclinación puede medirse como el ángulo θ que forma el vector normal a la superficie,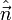 
con el campo.
Podemos observar que el número de líneas de campo que atraviesan las dos superficies es el mismo. Entonces el flujo a través de la superficie A2 es
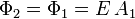
Podemos relacionar el área de las dos superficies usando la figura de la izquierda. Vemos que
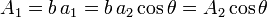
Por tanto, el flujo a través de la superficie inclinada es
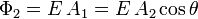
Esto se puede expresar en forma vectorial usando el vector unitario normal a la superficie. Para una superficie general, tenemos
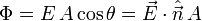
1.1.3 Campo no uniforme y superficie arbitraria
En el caso más general el campo eléctrico varía de un punto a otro de la superficie y ésta puede tener cualquier forma. Recurrimos entonces al cálculodiferencial. Dividimos la superficie en elementos de área, cada elemento con un vector normal 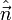y área dA. El flujo a través de cada elemento es
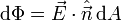
El flujo a través de toda la superficie es la suma de los flujos a través de cada elemento de área que podemos tomar en ella. Es decir
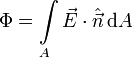
1.1.4 Superficie cerrada
Una superficie cerrada divide al espacio en dos partes, el interior y el exterior. Por convenio, el vector normal a una superficie cerrada se considera positivo cuando apunta hacia el exterior de la superficie. Al calcular el flujo del campo a través de una superficie cerrada se coloca un pequeño círculo en el signo integral
