Tres conductores esféricos concéntricos
De Laplace
| Línea 8: | Línea 8: | ||
==Coeficientes y circuito== | ==Coeficientes y circuito== | ||
| + | La forma más sencilla de calcular la matriz de coeficientes de capacidad e inducción es construyendo simultáneamente el circuito equivalente. | ||
| + | |||
| + | Tenemos tres conductores, a los que corresponden tres nodos en el circuito equivalente. | ||
| + | |||
| + | Entre cada par de nodos hay que situar un condensador. Sin embargo, el conductor “1” está apantallado del “3” por la corteza intermedia “2”. Por tanto, el condesnador correspondiente posee capacidad nula y puede omitirse del circuito | ||
| + | |||
| + | <center><math>\overline{C}_{13}=0</math></center> | ||
| + | |||
| + | El condensador <math>\overline{C}_{12}</math> que forman la esfera “1” y la corona “2” es un [[condensador esférico]] de radio interior 35 mm y exterior 45 mm, con capacidad | ||
| + | |||
| + | <center><math>\overline{C}_{12}=\frac{4\pi\varepsilon_0ab}{b-a}=\frac{(36\times 10^{-3})(36\times 10^{-3})}{9\times 10^9(45\times 10^{-3}-36\times 10^{-3})}\,\mathrm{F}=20\,\mathrm{pF}</math></center> | ||
| + | |||
| + | El condensador <math>\overline{C}_{23}</math> que forman la corona “2” y la corona “3” es también un condensador esférico, en este caso de radio interior 60 mm y exterior 120 mm, siendo su capacidad capacidad | ||
| + | |||
| + | <center><math>\overline{C}_{23}=\frac{4\pi\varepsilon_0a'b'}{b'-a'}=\frac{(60\times 10^{-3})(120\times 10^{-3})}{9\times 10^9(120\times 10^{-3}-60\times 10^{-3})}\,\mathrm{F}=\frac{40}{3}\,\mathrm{pF}=13.3\,\mathrm{pF}</math></center> | ||
| + | |||
| + | |||
| + | |||
| + | |||
==Cargas y potenciales iniciales== | ==Cargas y potenciales iniciales== | ||
==Cargas y potenciales finales== | ==Cargas y potenciales finales== | ||
==Variación en la energía== | ==Variación en la energía== | ||
[[Categoría:Problemas de electrostática en presencia de conductores]] | [[Categoría:Problemas de electrostática en presencia de conductores]] | ||
Revisión de 15:11 22 ene 2011
Contenido |
1 Enunciado
Se tienen un sistema formado por un conductor esférico “1” de radio 36 mm, una corona esférica “2” de radio interior 45 mm y exterior 60 mm y una corona esférica “3” de radio interior 120 mm y exterior 180 mm. Los tres conductores son concéntricos. No hay más conductores en el sistema.
- Suponiendo, en primer lugar, que los conductores se encuentran respectivamente a tensiones V1, V2 y V3 genéricas, diseñe el circuito equivalente mínimo y calcule los coeficientes de capacidad e inducción del sistema.
- Suponga el caso particular de que la esfera interior esté a tierra, la corona central esté aislada y almacene una carga de 6 nC y la exterior esté aislada y descargada. ¿Cuánto valen, en ese caso las cargas y tensiones de cada una de los tres conductores?
- Si en la situación anterior se conecta la corona exterior a tierra, ¿cuáles son las nuevas cargas y tensiones una vez que se alcanza el nuevo equilibrio electrostático?
- ¿Cuánto varía la energía almacenada en el sistema en el proceso anterior?
2 Coeficientes y circuito
La forma más sencilla de calcular la matriz de coeficientes de capacidad e inducción es construyendo simultáneamente el circuito equivalente.
Tenemos tres conductores, a los que corresponden tres nodos en el circuito equivalente.
Entre cada par de nodos hay que situar un condensador. Sin embargo, el conductor “1” está apantallado del “3” por la corteza intermedia “2”. Por tanto, el condesnador correspondiente posee capacidad nula y puede omitirse del circuito
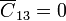
El condensador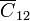 
que forman la esfera “1” y la corona “2” es un condensador esférico de radio interior 35 mm y exterior 45 mm, con capacidad
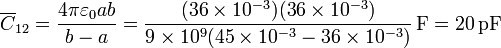
El condensador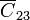 
que forman la corona “2” y la corona “3” es también un condensador esférico, en este caso de radio interior 60 mm y exterior 120 mm, siendo su capacidad capacidad
