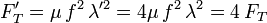Características de una onda en una cuerda
De Laplace
(Página creada con '== Enunciado == Una cuerda de masa 0.200 kg y 4.00 m de longitud se conecta a un diapasón que oscila con una frecuencia de 20.0 Hz. La amplitud de las osci…') |
|||
| Línea 50: | Línea 50: | ||
</math> | </math> | ||
</center> | </center> | ||
| + | |||
| + | |||
| + | |||
| + | [[Categoría:Problemas de movimiento ondulatorio]] | ||
última version al 13:39 12 ene 2011
1 Enunciado
Una cuerda de masa 0.200 kg y 4.00 m de longitud se conecta a un diapasón que oscila con una frecuencia de 20.0 Hz. La amplitud de las oscilaciones es de 1.00 cm. La onda transversal excitada en la cuerda resulta tener una longitud de onda de 10.0 cm. Determine la velocidad de la onda y la tensión aplicada a la cuerda. ¿Por qué factor es preciso multiplicar la tensión aplicada para que la longitud de onda se duplique?
2 Solución
A partir de la masa y la longitud de la cuerda su densidad lineal de masa es
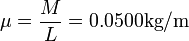
La velocidad de la onda en la cuerda es
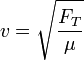
siendo FT la tensión en la cuerda. Por otro lado, como la onda es sinusoidal la velocidad puede escribirse también
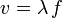
siendo λ la longitud de onda y f la frecuencia, que es la del diapasón. Así pues, la velocidad de la onda es
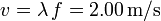
y la tensión es
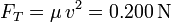
Queremos que la longitud de onda se duplique variando únicamente la tensión. Escribimos la longitud de onda directamente en función de la tensión
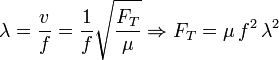
Si queremos que la nueva longitud de onda λ' sea el doble de la anterior tendremos