Observación desde plataforma giratoria

De Laplace

(Diferencias entre revisiones)

Revisión de 11:07 3 mar 2011

Contenido

1 Enunciado
2 Velocidad
3 Aceleración
4 Rapidez de impacto

1 Enunciado

Un individuo se encuentra sentado en el eje de una plataforma giratoria horizontal (sólido “1”) que rota con velocidad angular constante $Ω$ respecto al suelo (sólido “0”). Este persona arroja horizontalmente un hueso de aceituna desde una altura $h$ con velocidad $v 0$ . Despreciando el rozamiento del aire, de forma que el hueso se mueve exclusivamente por la acción de su peso, determine la velocidad y la aceleración que mide el observador rotatorio para cada instante. ¿En qué punto de la plataforma impacta el hueso? ¿Cuál es la rapidez relativa a la plataforma con la que golpea el suelo de ésta?

2 Velocidad

En este problema se trata de analizar cómo ve el mundo un observador en rotación. La velocidad y la aceleración que mide este observador no coinciden con las que mide uno situado en el suelo, no sometido a rotación.

Tenemos aquí tres sólidos: el hueso, que consideramos sólido “2”, el suelo exterior, que desempeña el papel de sólido intermedio “0” y la plataforma giratoria, que consideraremos como sólido de referencia “1”.

Desde el suelo	Desde la plataforma

Lo que va a ocurrir es que, mientras que para un observador situado en el suelo, el hueso va a a describir una parábola vertical, para el observador de la plataforma además se va a ir desviando lateralmente.

2.1 Movimiento {20}

Conocemos el movimiento del sólido “2” respecto al suelo “0”: describe un movimiento parabólico desde el punto inicial, ya que una vez que se separa del observador rotatorio, pierde la rotación que pudiera tener.

Si consideramos que plano del movimiento {20} del hueso se mueve en el $O X 0 Z 0$ , la posición instantánea del hueso es

$\left\{\begin{array}{rcl} x & = & v_0t \\ && \\ y & = & 0 \\ && \\ z & = & h-\displaystyle\frac{1}{2}gt^2\end{array}\right.\qquad\Rightarrow\qquad\overrightarrow{OH}=v_0 t \vec{\imath}_0+\left(h-\frac{1}{2}gt^2\right)\vec{k}_0$

Puesto que tenemos la posición en cada instante, podemos derivar para obtener la velocidad y la aceleración en el movimiento {20}

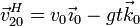
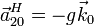
$\vec{v}^H_{20}=v_0\vec{\imath}_0-g t \vec{k}_0$ $\vec{a}^H_{20}=-g\vec{k}_0$

2.2 Movimiento {01}

Si el observador está rotando con velocidad angular $Ω$ en sentido antihorario percibirá que el hueso de aceituna gira en sentido horario respecto a él. La velocidad angular de este movimiento es

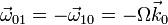
$\vec{\omega}_{01}=-\vec{\omega}_{10}=-\Omega\vec{k}_0$

La velocidad de arrastre depende de la distancia, como corresponde a una rotación respecto a un eje fijo

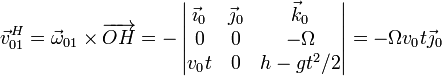
$\vec{v}^H_{01}=\vec{\omega}_{01}\times\overrightarrow{OH}=-\left|\begin{matrix}\vec{\imath}_0 & \vec{\jmath}_0 & \vec{k}_0 \\ 0 & 0 & -\Omega\\ v_0 t & 0 & h-gt^2/2\end{matrix}\right| = -\Omega v_0 t \vec{\jmath}_0$

Nótese que hemos expresado esta velocidad en los ejes ligados al sólido 0 (el suelo).

2.3 Movimiento {21}

Sumando las dos velocidades anteriores obtenemos la velocidad medida por el observador en rotación

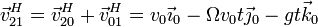
$\vec{v}^H_{21}=\vec{v}^H_{20}+\vec{v}^H_{01}=v_0\vec{\imath}_0-\Omega v_0 t \vec{\jmath}_0-g t\vec{k}_0$

Podría pensarse que el observador móvil ve un movimiento de aceleración constante (ya que el nuevo término se parece a la componente vertical). Sin embargo no es así, ya que hemos expresado el resultado en unos ejes ligados al suelo “0”, que para el observador giratorio son unos ejes móviles.

Para expresar el vector velocidad en una base ligada a la plataforma en rotación, debemos relacionar las bases respectivas. Tenemos que el vector $\vec{k}$ es el mismo para ambas bases. Para los otros dos vectores tenemos las relaciones

$\begin{array}{rcl}\vec{\imath}_0 & = & \cos(\Omega t) \vec{\imath}_1 -\mathrm{sen}(\Omega t)\vec{\jmath}_1 \\ \vec{\jmath}_0 & = & \mathrm{sen}(\Omega t)\vec{\imath}_1 + \cos(\Omega t)\vec{\jmath}_1\end{array}$

lo que nos da la velocidad

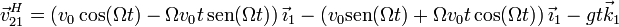
$\vec{v}^H_{21}=\left(v_0\cos(\Omega t)-\Omega v_0 t\,\mathrm{sen}(\Omega t)\right)\vec{\imath}_1-\left(v_0\mathrm{sen}(\Omega t)+\Omega v_0 t\cos(\Omega t)\right)\vec{\imath}_1-g t\vec{k}_1$

que no es para nada la ecuación de un movimiento de aceleración constante.

3 Aceleración

Del mismo modo que para la velocidad, tenemos la aceleración.

3.1 En el movimiento {20}

La aceleración del hueso respecto al suelo es constante

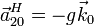
$\vec{a}^H_{20}=-g\vec{k}_0$

3.2 En el movimiento {01}

Para la aceleración de arrastre empleamos la expresión del campo de aceleraciones de un sólido

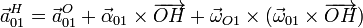
$\vec{a}^H_{01}=\vec{a}^O_{01} +\vec{\alpha}_{01}\times\overrightarrow{OH}+\vec{\omega}_{O1}\times(\vec{\omega}_{01}\times\overrightarrow{OH})$

En este caso, la aceleración de un punto del eje es nula, por ser éste fijo. También se anula la aceleración angular, por rotar la plataforma con velocidad angular constante. Para el último término resulta

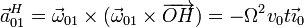
$\vec{a}^H_{01}=\vec{\omega}_{01}\times(\vec{\omega}_{01}\times\overrightarrow{OH})=-\Omega^2v_0t\vec{\imath}_0$

Vemos que resulta una aceleración radial hacia adentro, como corresponde a que en este movimiento haya una rotación alrededor del eje.

De nuevo, hay que señalar que este resultado lo hemos expresado usando los ejes ligados al suelo, que para el observador rotatorio son ejes móviles.

3.3 En el movimiento {21}

Por último, según el teorema de Coriolis tenemos

$\vec{a}^H_{21}=\vec{a}^H_{20}+\vec{a}^H_{01}+2\vec{\omega}_{01}\times\vec{v}^H_{20}$

Nos queda por hallar el tercer sumando

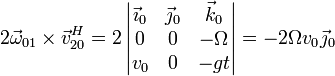
$2\vec{\omega}_{01}\times\vec{v}^H_{20}=2\left|\begin{matrix}\vec{\imath}_0 & \vec{\jmath}_0 & \vec{k}_0 \\ 0 & 0 & -\Omega \\ v_0 & 0 & -g t\end{matrix}\right| = -2\Omega v_0\vec{\jmath}_0$

Sumando los tres términos

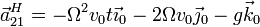
$\vec{a}^H_{21}=-\Omega^2v_0t\vec{\imath}_0-2\Omega v_0\vec{\jmath}_0-g\vec{k}_0$

De nuevo, si queremos expresar este resultado en la base ligada a la plataforma giratoria queda

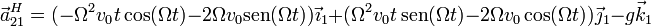
$\vec{a}^H_{21}=(-\Omega^2v_0t\cos(\Omega t)-2\Omega v_0\mathrm{sen}(\Omega t))\vec{\imath}_1+(\Omega^2v_0t\,\mathrm{sen}(\Omega t)-2\Omega v_0\cos(\Omega t))\vec{\jmath}_1-g\vec{k}_1$

4 Rapidez de impacto

La celeridad con la que impacta la plataforma lo da el modulo de la velocidad {21}

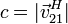
$c = |\vec{v}^H_{21}|$

en el momento del impacto. Este se produce cuando $z = 0$ , lo que ocurre en el instante

$0 = h-\frac{1}{2}gt_i^2\qquad\Rightarrow\qquad t_i = \sqrt{\frac{2h}{g}}$

y la velocidad en ese momento es

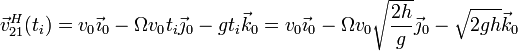
$\vec{v}^H_{21}(t_i)=v_0\vec{\imath}_0-\Omega v_0 t_i \vec{\jmath}_0-g t_i\vec{k}_0=v_0\vec{\imath}_0-\Omega v_0 \sqrt{\frac{2h}{g}} \vec{\jmath}_0-\sqrt{2gh}\vec{k}_0$

con módulo

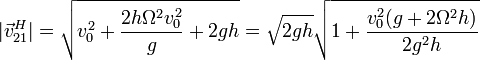
$|\vec{v}^H_{21}| = \sqrt{v_0^2 + \frac{2h\Omega^2v_0^2}{g}+2gh} = \sqrt{2gh}\sqrt{1+ \frac{v_0^2(g+2\Omega^2h)}{2g^2h}}$

Nótese que para hallar el módulo no necesitamos expresar el vector en la base móvil.

Esta rapidez es mayor que la que tendría si impactara contra el suelo inmóvil. Para un observador en el suelo, esto se debe a que, aunque el hueso cae con la velocidad habitual, la plataforma “va a su encuentro”, aumentando la celeridad de impacto. Para el observador giratorio, se debe a que el hueso no cae haciendo una parábola, sino que también tiene un movimiento lateral que hay que incluir en la velocidad.

@@ Línea 55: / Línea 55: @@
 <center><math>\vec{v}^H_{21}=\left(v_0\cos(\Omega t)-\Omega v_0 t\,\mathrm{sen}(\Omega t)\right)\vec{\imath}_1-\left(v_0\mathrm{sen}(\Omega t)+\Omega v_0 t\cos(\Omega t)\right)\vec{\imath}_1-g t\vec{k}_1</math></center>
-que no es para nada la ecuación un movimiento de aceleración constante.
+que no es para nada la ecuación de un movimiento de aceleración constante.
 ==Aceleración==

Observación desde plataforma giratoria

De Laplace

Revisión de 11:07 3 mar 2011

Contenido

1 Enunciado

2 Velocidad

2.1 Movimiento {20}

2.2 Movimiento {01}

2.3 Movimiento {21}

3 Aceleración

3.1 En el movimiento {20}

3.2 En el movimiento {01}

3.3 En el movimiento {21}

4 Rapidez de impacto

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES