Observación desde plataforma giratoria

De Laplace

(Diferencias entre revisiones)

Revisión de 22:26 23 nov 2010

Contenido

1 Enunciado
2 Velocidad
3 Aceleración

1 Enunciado

Un individuo se encuentra sentado en el eje de una plataforma giratoria horizontal (sólido “1”) que rota con velocidad angular constante $Ω$ respecto al suelo (sólido “0”). Este persona arroja horizontalmente un hueso de aceituna desde una altura $h$ con velocidad $v 0$ . Despreciando el rozamiento del aire, de forma que el hueso se mueve exclusivamente por la acción de su peso, determine la velocidad y la aceleración que mide el observador rotatorio para cada instante. ¿En qué punto de la plataforma impacta el hueso? ¿Cuál es la rapidez relativa a la plataforma con la que golpea el suelo de ésta?

2 Velocidad

En este problema se trata de analizar cómo ve el mundo un observador en rotación. La velocidad y la aceleración que mide este observador no coinciden con las que mide uno situado en el suelo, no sometido a rotación.

Tenemos aquí tres sólidos: el hueso, que consideramos sólido “2”, el suelo exterior, que desempeña el papel de sólido intermedio “0” y la plataforma giratoria, que consideraremos como sólido de referencia “1”.

2.1 Movimiento {20}

Conocemos el movimiento del sólido “2” respecto al suelo “0”: describe un movimiento parabólico desde el punto inicial, ya que una vez que se separa del observador rotatorio, pierde la rotación que pudiera tener.

Si consideramos que plano del movimiento {20} del hueso se mueve en el $O X 0 Z 0$ , la posición instantánea del hueso es

$\left\{\begin{array}{rcl} x & = & v_0t \\ && \\ y & = & 0 \\ && \\ z & = & h-\displaystyle\frac{1}{2}gt^2\end{array}\right.\qquad\Rightarrow\qquad\overrightarrow{OH}=v_0 t \vec{\imath}_0+\left(h-\frac{1}{2}gt^2\right)\vec{k}_0$

Puesto que tenemos la posición en cada instante, podemos derivar para obtener la velocidad y la aceleración en el movimiento {20}

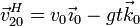
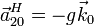
$\vec{v}^H_{20}=v_0\vec{\imath}_0-g t \vec{k}_0$ $\vec{a}^H_{20}=-g\vec{k}_0$

2.2 Movimiento {01}

Si el observador está rotando con velocidad angular $Ω$ en sentido horario percibirá que el hueso de aceituna gira en sentido antihorario respecto a él. La velocidad angular de este movimiento es

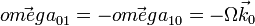
$\vec{omega}_{01}=-\vec{omega}_{10}=-\Omega\vec{k}_0$

La velocidad de arrastre depende de la distancia, como corresponde a una rotación respecto a un eje fijo

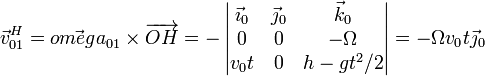
$\vec{v}^H_{01}=\vec{omega}_{01}\times\overrightarrow{OH}=-\left|\begin{matrix}\vec{\imath}_0 & \vec{\jmath}_0 & \vec{k}_0 \\ 0 & 0 & -\Omega\\ v_0 t & 0 & h-gt^2/2\end{matrix}\right| = -\Omega v_0 t \vec{\jmath}_0$

Nótese que hemos expresado esta velocidad en los ejes ligados al sólido 0 (el suelo).

2.3 Movimiento {21}

Sumando las dos velocidades anteriores obtenemos la velocidad medida por el observador en rotación

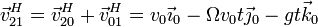
$\vec{v}^H_{21}=\vec{v}^H_{20}+\vec{v}^H_{01}=v_0\vec{\imath}_0-\Omega v_0 t \vec{\jmath}_0-g t\vec{k}_0$

Podría pensarse que el observador móvil ve un movimiento de aceleración constante (ya que el nuevo término se parece a la componente vertical). Sin embargo no es así, ya que hemos expresado el resultado en unos ejes ligados al suelo “0”, que para el observador giratorio son unos ejes móviles.

Para expresar el vector velocidad en una base ligada a la plataforma en rotación, debemos relacionar las bases respectivas. Tenemos que el vector $\vec{k}$ es el mismo para ambas bases. Para los otros dos vectores tenemos las relaciones

$\begin{array}{rcl}\vec{\imath}_0 & = & \cos(\Omega t) \vec{\imath}_1 -\mathrm{sen}(\Omega t)\vec{\jmath}_1 \\ \vec{\jmath}_0 & = & \mathrm{sen}(\Omega t)\vec{\imath}_1 + \cos(\Omega t)\vec{\jmath}_1\end{array}$

lo que nos da la velocidad

$\vec{v}^H_{21}=\left(v_0\cos(\Omega t)-\Omega v_0 t\,\mathrm{sen}(\Omega t)\right)\vec{\imath}_1+\left(-v_0\mathrm{sen}(\Omega t)-\Omega v_0 t\cos(\Omega t)\right)\vec{\imath}_0-g t\vec{k}_0$

3 Aceleración

@@ Línea 39: / Línea 39: @@
 <center><math>\begin{array}{rcl}\vec{\imath}_0 & = &  \cos(\Omega t) \vec{\imath}_1 -\mathrm{sen}(\Omega t)\vec{\jmath}_1 \\
-\vec{\jmath}_0 & = &  \mathrm{sen}(\Omega t)\ve{\imath}_1 + \cos(\Omega t)\vec{\jmath}_1\end{array}</math></center>
+\vec{\jmath}_0 & = &  \mathrm{sen}(\Omega t)\vec{\imath}_1 + \cos(\Omega t)\vec{\jmath}_1\end{array}</math></center>
 lo que nos da la velocidad

Observación desde plataforma giratoria

De Laplace

Revisión de 22:26 23 nov 2010

Contenido

1 Enunciado

2 Velocidad

2.1 Movimiento {20}

2.2 Movimiento {01}

2.3 Movimiento {21}

3 Aceleración

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES