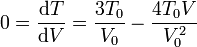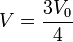Compresión lineal
De Laplace
(→Trabajo) |
|||
| Línea 44: | Línea 44: | ||
<center><math>W= -\int_{V_0}^{V_0/2} \left(3p_0-\frac{2p_0V}{V_0}\right)\mathrm{d}V = -\left.3p_0V\right|_{V_0}^{V_0/2}+\left.\frac{p_0V^2}{V_0}\right|_{V_0}^{V_0/2} = \frac{3p_0V_0}{4}</math></center> | <center><math>W= -\int_{V_0}^{V_0/2} \left(3p_0-\frac{2p_0V}{V_0}\right)\mathrm{d}V = -\left.3p_0V\right|_{V_0}^{V_0/2}+\left.\frac{p_0V^2}{V_0}\right|_{V_0}^{V_0/2} = \frac{3p_0V_0}{4}</math></center> | ||
| - | Es muy fácil llegar a este resultado de forma gráfica, ya que el área bajo la curva es la de un trapecio de altura | + | Es muy fácil llegar a este resultado de forma gráfica, ya que el área bajo la curva es la de un trapecio de altura <math>V_0/2</math>, base menor <math>p_0</math> y base mayor <math>2p_0</math>. El área de este trapecio es |
<center><math>W = \frac{1}{2}\left(\frac{V_0}{2}\right)\left(2p_0+p_0\right) = \frac{3p_0V_0}{4}</math></center> | <center><math>W = \frac{1}{2}\left(\frac{V_0}{2}\right)\left(2p_0+p_0\right) = \frac{3p_0V_0}{4}</math></center> | ||
| + | |||
===Energía interna=== | ===Energía interna=== | ||
Por tratarse de un gas ideal, la variación en la energía interna solo depende de la temperatura inicial y la final | Por tratarse de un gas ideal, la variación en la energía interna solo depende de la temperatura inicial y la final | ||
Revisión de 17:13 16 nov 2010
Contenido |
1 Enunciado
Se tiene un volumen V0 de un gas ideal diatómico a una presión p0 y una temperatura T0 encerrado en un recipiente con un pistón móvil. Este gas se comprime reversiblemente según la ley
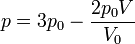
reduciéndose el volumen hasta V0 / 2.
- Trace la gráfica del proceso en un diagrama PV.
- Calcule la temperatura final del proceso.
- Calcule el trabajo neto realizado sobre el gas, la variación de su energía interna y el calor que entra en el gas durante el proceso.
- ¿Para qué volumen durante el proceso la temperatura es máxima? Halle el valor de esta temperatura máxima.
- Separando el proceso en dos: uno hasta que alcanza la temperatura máxima y otro de ahí hasta el final, halle W, ΔU y Q en cada uno de los dos subprocesos.
2 Representación gráfica
Dado que la presión depende del volumen en la forma
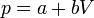
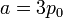

es claro que la gráfica del proceso es un segmento rectilíneo. El punto inicial del segmento es (p0,V0) y el punto final corresponde a V = V0 / 2 y a la presión
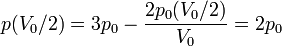
Por tanto el volumen final es la mitad del inicial, mientras que la presión es el doble.
3 Temperatura final
Obtenemos la temperatura final a partir de la ecuación de los gases ideales. Inicialmente tenemos
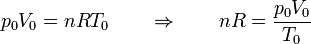
En el estado final
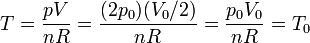
Por tanto, la temperatura final es igual a la inicial.
4 Trabajo, energía y calor
4.1 Trabajo
El trabajo realizado sobre el gas en un proceso reversible es igual a la integral
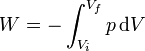
En nuestro caso
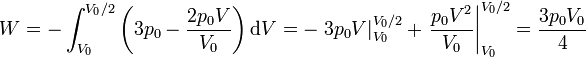
Es muy fácil llegar a este resultado de forma gráfica, ya que el área bajo la curva es la de un trapecio de altura V0 / 2, base menor p0 y base mayor 2p0. El área de este trapecio es
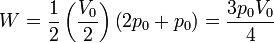
4.2 Energía interna
Por tratarse de un gas ideal, la variación en la energía interna solo depende de la temperatura inicial y la final
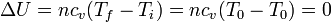
Puesto que la temperatura inicial y la final son la misma, no hay variación en la energía interna del gas.
4.3 Calor
Una vez que tenemos el trabajo y la variación de la energía interna, hallamos el calor empleando el primer principio de la termodinámica
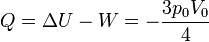
En este proceso se realiza trabajo, pero puesto que la temperatura del sistema es la misma al principio y al final, ese trabajo sale del sistema en forma de calor. Este proceso, no obstante, no es isotermo, ya que la temperatura del sistema cambia en los estados intermedios.
5 Temperatura máxima
La temperatura del gas en cada estado del proceso la hallamos por la ley de los gases ideales
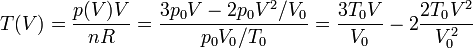
La gráfica de esta función tiene una forma parabólica, con un máximo en algún punto intermedio entre el estado inicial y el final. Hallamos la posición del máximo igualando la derivada a cero.