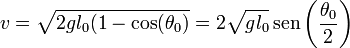3.3. Tensión de un péndulo
De Laplace
(→Velocidad máxima) |
(→Velocidad máxima) |
||
| Línea 27: | Línea 27: | ||
y esto nos da la velocidad | y esto nos da la velocidad | ||
| - | <center><math>v = \sqrt{2gl_0(1-\cos(\theta_0)} = 2\sqrt{gl_0}\mathrm{sen}\left(\frac{\theta_0}{2}\right)</math></center> | + | <center><math>v = \sqrt{2gl_0(1-\cos(\theta_0)} = 2\sqrt{gl_0}\,\mathrm{sen}\left(\frac{\theta_0}{2}\right)</math></center> |
==Tensión== | ==Tensión== | ||
[[Categoría:Problemas de dinámica del punto material (G.I.T.I.)]] | [[Categoría:Problemas de dinámica del punto material (G.I.T.I.)]] | ||
Revisión de 20:18 20 oct 2010
1 Enunciado
Empleando la ley de conservación de la energía, determine la velocidad con la que un péndulo simple de masa m y longitud l0 pasa por su punto más bajo, como función del ángulo máximo θ0 con el que se separa de la vertical.
Determine la tensión de la cuerda en el punto más bajo y en el punto de máxima separación de la vertical.
2 Velocidad máxima
Podemos hallar la velocidad máxima a partir de la ley de conservación de la energía mecánica. La partícula está sometida a dos fuerzas: su peso y la tensión de la cuerda.
La tensión va siempre en la dirección de la cuerda y por tanto es perpendicular al movimiento de la partícula. Por ello, no realiza trabajo sobre ella, y solo debemos considerar el trabajo debido al peso. Puesto que el peso deriva de una energía potencial
podemos escribir la ley de conservación de la energía mecánica
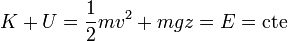
En el caso de las oscilaciones de un péndulo, si medimos las alturas desde el punto más bajo de las oscilaciones, cuando se halla en el punto de máxima separación de la vertical se encuentra a una altura
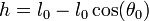
siendo su velocidad nula (si no, el ángulo no sería máximo). En el punto más bajo, su altura es nula y tiene una velocidad v. Igualando la energía mecánica en un punto con la del otro nos queda
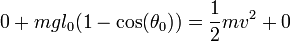
y esto nos da la velocidad