Cálculo de base dual
De Laplace
(→Ortogonalidad) |
(→Componentes de un vector) |
||
| Línea 63: | Línea 63: | ||
==Componentes de un vector== | ==Componentes de un vector== | ||
| + | La ortogonalidad entre las bases duales permite hallar las componentes de un vector en una base a partir de las proyecciones sobre la otra. | ||
| + | |||
| + | Supongamos un vector <math>\vec{F}</math> que conocemos y que es expresable como combinación lineal de la base <math>B_1</math> | ||
| + | |||
| + | <center><math>\vec{F}=F_1\vec{v}_1+F_2\vec{v}_2+F_3\vec{v}_3</math></center> | ||
| + | |||
| + | aunque estas componentes <math>F_i</math> son desconocidas por ahora y es lo que nos gustaría calcular. | ||
| + | |||
| + | Para hallar las componentes individuales en esta base, podríamos multiplicar escalarmente por la propia base. Pero dado que esta base no es ortonormal, lo que obtenemos de este modo es un sistema de tres ecuaciones con tres incógnitas que, aunque es fácil de resolver, requiere bastantes operaciones. | ||
| + | |||
| + | Si en lugar de multiplicar por los vectores de la base B_1 lo hacemos por los de la base B_2 obtenemos en cambio | ||
| + | |||
| + | <center><math>\vec{F}\cdot\vec{w}_1=F_1\overbrace{\vec{v}_1\cdot\vec{w}_1}^{=1}+F_2\overbrace{\vec{v}_2\cdot\vec{w}_1}^{=0}+F_3\overbrace{\vec{v}_3\cdot\vec{w}_1}^{=0}=F_1</math></center> | ||
| + | |||
| + | <center><math>\vec{F}\cdot\vec{w}_2=F_1\overbrace{\vec{v}_1\cdot\vec{w}_2}^{=0}+F_2\overbrace{\vec{v}_2\cdot\vec{w}_2}^{=1}+F_3\overbrace{\vec{v}_3\cdot\vec{w}_2}^{=0}=F_2</math></center> | ||
| + | |||
| + | <center><math>\vec{F}\cdot\vec{w}_3=F_1\overbrace{\vec{v}_1\cdot\vec{w}_3}^{=0}+F_2\overbrace{\vec{v}_2\cdot\vec{w}_3}^{=0}+F_3\overbrace{\vec{v}_3\cdot\vec{w}_3}^{=1}=F_3</math></center> | ||
| + | |||
| + | Por tanto, multiplicando escalarmente por los vectores de la base dual obtenemos directamente las componentes en la base original. | ||
| + | |||
| + | Dada la simetría entre las bases, el procedimiento funciona también en sentido contrario. | ||
| + | |||
==Caso particular== | ==Caso particular== | ||
==Ejemplo de cálculo de componentes== | ==Ejemplo de cálculo de componentes== | ||
[[Categoría:Problemas de vectores libres (G.I.T.I.)]] | [[Categoría:Problemas de vectores libres (G.I.T.I.)]] | ||
Revisión de 11:00 26 sep 2010
Contenido[ocultar] |
1 Enunciado
Sea 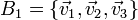 una base vectorial arbitraria. Sean
una base vectorial arbitraria. Sean 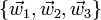 tres vectores definidos por
tres vectores definidos por
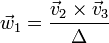
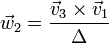


- 1. Demuestre que el conjunto
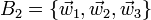 es también una base (llamada base dual de B1). ¿Cuánto vale el producto mixto de sus vectores?
es también una base (llamada base dual de B1). ¿Cuánto vale el producto mixto de sus vectores?
- 2. Pruebe que se cumple
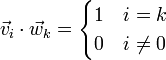
- 3. Demuestre que las componentes de un vector en la base B1 pueden calcularse proyectando sobre la base B2, esto es, si
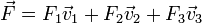
- la componente k viene dada por
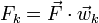
- 4. Halle la base dual de la base
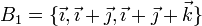
- 5. Calcule las componentes del vector
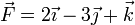
- en las bases del apartado anterior.
2 Carácter de base
En el espacio de tridimensional ordinario, cualquier conjunto de tres vectores linealmente independientes constituye una base.
Para demostrar la independencia lineal basta probar que el producto mixto de los tres vectores es nulo. Por tanto debemos hallar
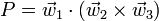
Sustituyendo las definiciones de cada uno de los vectores
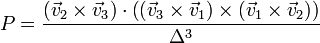
Para el triple producto vectorial tenemos, aplicando las propiedades del doble producto vectorial
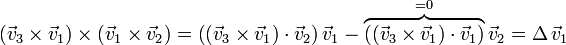
y por tanto el producto mixto de los tres vectores vale

Por tanto, si B1 es una base, B2 también lo es y el producto mixto de los vectores de B2 es el inverso de los de B1.
3 Ortogonalidad
Los vectores de la base B1 no son ortogonales entre sí, como tampoco lo son los de la base B2. sin embargo, los de una de las bases son ortogonales a los de la otra (y viceversa).
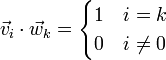
Dada la simetría de la definición de los vectores de B2 nos basta con probarlo para el primero de sus vectores. Multiplicándolo por cada uno de los vectores de B_1 tenemos, para el primero
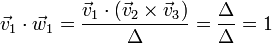
para el segundo y el tercero, aplicando que el producto vectorial es ortogonal a los dos vectores que lo forman
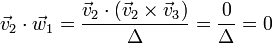

Si se opera con 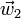 o con
o con 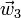 el resultado es análogo.
el resultado es análogo.
4 Componentes de un vector
La ortogonalidad entre las bases duales permite hallar las componentes de un vector en una base a partir de las proyecciones sobre la otra.
Supongamos un vector  que conocemos y que es expresable como combinación lineal de la base B1
que conocemos y que es expresable como combinación lineal de la base B1
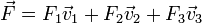
aunque estas componentes Fi son desconocidas por ahora y es lo que nos gustaría calcular.
Para hallar las componentes individuales en esta base, podríamos multiplicar escalarmente por la propia base. Pero dado que esta base no es ortonormal, lo que obtenemos de este modo es un sistema de tres ecuaciones con tres incógnitas que, aunque es fácil de resolver, requiere bastantes operaciones.
Si en lugar de multiplicar por los vectores de la base B_1 lo hacemos por los de la base B_2 obtenemos en cambio
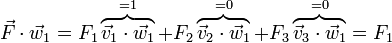
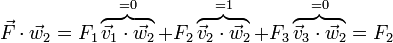
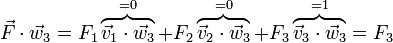
Por tanto, multiplicando escalarmente por los vectores de la base dual obtenemos directamente las componentes en la base original.
Dada la simetría entre las bases, el procedimiento funciona también en sentido contrario.





