1.10. Volumen de un paralelepípedo
De Laplace
(Diferencias entre revisiones)
(→Primer volumen) |
(→Primer volumen) |
||
| Línea 21: | Línea 21: | ||
Al ser positivo, este es el volumen del paralelepípedo. | Al ser positivo, este es el volumen del paralelepípedo. | ||
| - | <center><math>V = 20\,</math></center> | + | <center><math>V = 20\,</math>m<math>^3</math></center> |
==Segundo volumen== | ==Segundo volumen== | ||
==Volumen del tetraedro== | ==Volumen del tetraedro== | ||
[[Categoría:Problemas de vectores libres (G.I.T.I.)]] | [[Categoría:Problemas de vectores libres (G.I.T.I.)]] | ||
Revisión de 17:02 24 sep 2010
Contenido |
1 Enunciado
Sean los puntos de coordenadas (en el SI) O(1,0,2), A(3,2,4), B(2,6,8) y C(2, − 3,1). Determine el volumen del paralelepípedo definido por los vectores  ,
, 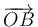 y
y  .
.
Halle del mismo modo el volumen del paralelepípedo definido por los vectores  ,
, 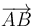 y
y 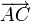 .
.
Calcule igualmente el volumen del tetraedro irregular definido por estos cuatro puntos.
2 Primer volumen
El volumen de un paralelepípedo se calcula como el producto mixto (sin signo) de los tres vectores que definen el paralelepíedo.
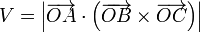
En nuestro caso los vectores los obtenemos hallando las diferencias entre las coordenadas de cada par de puntos
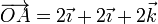
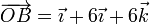
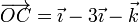
de forma que el producto mixto lo da el determinante

Al ser positivo, este es el volumen del paralelepípedo.
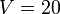 m3
m3




