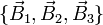Entrar Página Discusión Historial Go to the site toolbox

Problemas de vectores libres (G.I.T.I.)

De Laplace

(Diferencias entre revisiones)
(→Formulas posiblemente incorrectas)
(→Formulas posiblemente incorrectas)
Línea 17: Línea 17:
:(b) <math>\vec{F}\times(\vec{v}\times\vec{a}) = (\vec{p}\cdot\vec{a})\times\vec{a}</math>
:(b) <math>\vec{F}\times(\vec{v}\times\vec{a}) = (\vec{p}\cdot\vec{a})\times\vec{a}</math>
-
:(c) <math>\frac{\vec{L}}{R} = \vec{F}{m}-\vec{v}</math>
+
:(c) <math>\frac{\vec{L}}{R} = \vec{F}t-\vec{v}</math>
:(d) <math>(\vec{r}\times\vec{p})\cdot\vec{L} = R(\vec{r}\cdot\vec{p})\vec{p}</math>
:(d) <math>(\vec{r}\times\vec{p})\cdot\vec{L} = R(\vec{r}\cdot\vec{p})\vec{p}</math>

Revisión de 17:27 11 sep 2010

1 Ejemplo de construcción de una base

Dados los vectores

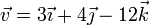
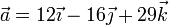
\vec{v}=3\vec{\imath}+4\vec{\jmath}-12\vec{k}        \vec{a}=12\vec{\imath}-16\vec{\jmath}+29\vec{k}

Construya una base ortonormal dextrógira, tal que

  • El primer vector vaya en la dirección de \vec{v}
  • El segundo esté contenido en el plano definido por \vec{v} y \vec{a}
  • El tercero sea perpendicular a los dos anteriores, y orientado según la regla de la mano derecha.

2 Formulas posiblemente incorrectas

De las siguientes expresiones, indique cuáles son necesariamente incorrectas. Aquí las diferentes letras representan las magnitudes definidas en el problema de ejemplos de análisis dimensional, R es una distancia y \vec{r} el vector de posición; t es el tiempo:

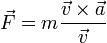
(a) \vec{F} = m\frac{\vec{v}\times\vec{a}}{\vec{v}}
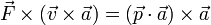
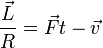
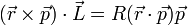
(b) \vec{F}\times(\vec{v}\times\vec{a}) = (\vec{p}\cdot\vec{a})\times\vec{a}
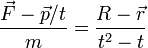
(c) \frac{\vec{L}}{R} = \vec{F}t-\vec{v}
(d) (\vec{r}\times\vec{p})\cdot\vec{L} = R(\vec{r}\cdot\vec{p})\vec{p}
(e) \frac{\vec{F}-\vec{p}/t}{m} = \frac{R-\vec{r}}{t^2-t}
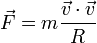
(f) \vec{F} = m\frac{\vec{v}\cdot\vec{v}}{R}
(g) |\vec{L}| = \vec{r}\cdot\vec{p}
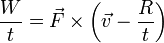
(h) \frac{W}{t} = \vec{F}\times\left(\vec{v}-\frac{R}{t}\right)

3 Base dual

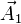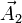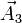Sean \vec{A}_1, \vec{A}_2 y \vec{A}_3 tras vectores linealmente independientes. Sean \{\vec{B}_1,\vec{B}_2,\vec{B}_3\}

Obtenido de "http://tesla.us.es/wiki/index.php/Problemas_de_vectores_libres_(G.I.T.I.)"

Herramientas:

Herramientas personales
TOOLBOX
LANGUAGES
licencia de Creative Commons
 Aviso legal - Acerca de Laplace