1.1. Ejemplos de análisis dimensional

De Laplace

(Diferencias entre revisiones)

Revisión de 14:33 8 sep 2010

1 Enunciado

A partir de las relaciones definitorias

Velocidad	Cantidad de movimiento	Aceleración	Fuerza
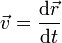
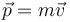
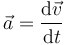
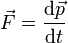
$\vec{v}=\frac{\mathrm{d}\vec{r}}{\mathrm{d}t}$	$\vec{p}=m\vec{v}$	$\vec{a}=\frac{\mathrm{d}\vec{v}}{\mathrm{d}t}$	$\vec{F}=\frac{\mathrm{d}\vec{p}}{\mathrm{d}t}$
Trabajo	Potencia	Momento cinético	Momento de una fuerza
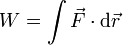
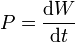
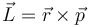
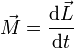
$W=\int\vec{F}\cdot\mathrm{d}\vec{r}$	$P=\frac{\mathrm{d}W}{\mathrm{d}t}$	$\vec{L}=\vec{r}\times\vec{p}$	$\vec{M}=\frac{\mathrm{d}\vec{L}}{\mathrm{d}t}$

determine las ecuaciones dimensionales de estas magnitudes, así como sus unidades en el SI en función de las unidades fundamentales de este sistema.

2 Velocidad

La velocidad se define como la derivada de la posición respecto al tiempo. Una derivada no es más que un cociente entre dos cantidades muy pequeñas y por tanto sus dimensiones serán las del numerador divididas por las del denominador, esto es,

$[v] = \frac{[r]}{[t]} = L T^{-1}$

3 Cantidad de movimiento

La cantidad de movimiento es el producto de la masa por la velocidad, por lo que sus dimensiones serán las del producto de estas dos cantidades:

$[p]= [m][v]= MLT^{-1}\,$

La unidad SI de la cantidad de movimiento será

$u_p = 1\,\frac{\mathrm{kg}\cdot\mathrm{m}}{\mathrm{s}}/math></center> ==Aceleración== ==Fuerza== ==Trabajo== ==Potencia== ==Momento cinético== ==Momento de una fuerza== [[Categoría:Problemas de metrología]]$

@@ Línea 39: / Línea 39: @@
 La unidad SI de la cantidad de movimiento será
-<center><math>u_p = 1\,\frac{\mathrm{kg}\cdot\mathrm{m}}{\mathrm{s}</math></center>
+<center><math>u_p = 1\,\frac{\mathrm{kg}\cdot\mathrm{m}}{\mathrm{s}}/math></center>
 ==Aceleración==

1.1. Ejemplos de análisis dimensional

De Laplace

Revisión de 14:33 8 sep 2010

1 Enunciado

2 Velocidad

3 Cantidad de movimiento

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES