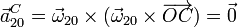Entrar Página Discusión Historial Go to the site toolbox

Rotación de un disco inclinado

De Laplace

(Diferencias entre revisiones)
(→Movimiento de arrastre)
(→Movimiento relativo)
Línea 143: Línea 143:
;Punto A:
;Punto A:
-
<center><math>\vec{a}^A_{20}=\vec{\omega}_{20}\times(\vec{\omega}_{20}\times\overrightarrow{OA})=-\frac{4\pi^2L^2}{a^2T^2}\sqrt{L^2+a^2}\vec{\imath}</math></center>
+
<center><math>\vec{a}^A_{20}=\vec{\omega}_{20}\times(\vec{\omega}_{20}\times\overrightarrow{OA})=-\frac{4\pi^2L^2}{a T^2}\sqrt{L^2+a^2}(a\vec{\imath}-L\vec{k})</math></center>
;Punto B:
;Punto B:

Revisión de 16:38 17 ago 2010

Contenido

1 Enunciado

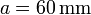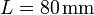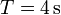Un disco de radio a=60\,\mathrm{mm} en cuyo eje está ensartada una barra de longitud L=80\,\mathrm{mm} se halla apoyada en el extremo de la barra y en el borde del disco. El disco rueda sobre una superficie horizontal, manteniendo fija la posición del extremo de la barra. El giro es uniforme, de forma que el centro del disco completa una revolución cada T=4\,\mathrm{s}.

Se consideran como sólido 1 la superficie horizontal, como sólido 0 la barra y como sólido 2 el disco. En un instante dado de toman los ejes del sistema 0 y 1 coincidentes y tales que OZ es la normal al plano horizontal que pasa por O, el extremo de la barra, OX es la recta horizontal que pasa por O y por A, el punto de contacto del disco con la mesa, y OY es la normal a los otros dos ejes.

  1. Determine la posición de los ejes instantáneos de rotación en los movimientos absoluto {21}, relativo {20} y de arrastre {01}.
  2. Halle las velocidades de los puntos A (de contacto del disco con la mesa), B (diametralmente opuesto a A) y C (centro del disco), en los tres movimientos.
  3. Calcule la aceleración de los mismos puntos.

2 Ejes instantáneos de rotación

Puesto que tenemos un punto fijo en los tres movimientos, que es el punto O de contacto de la barra con la mesa, los movimientos absoluto, relativo y de arrastre son sendas rotaciones puras, cuyos ejes instantáneos de rotación pasan por el punto O.

La orientación de cada eje la da la velocidad angular de cada movimiento.

Movimiento absoluto {21}
En el movimiento del disco respecto a la mesa tenemos dos puntos instantáneamente en reposo, el ya mencionado punto O y el punto A de contacto del disco con la mesa, por estar rodando el disco sobre la mesa. Por tanto el eje instantáneo de rotación es la recta horizontal que pasa por estos dos puntos (que hemos tomado como eje OX tanto en el sólido 0 como en el 1) y la velocidad angular de este movimiento es de la forma
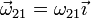
\vec{\omega}_{21}=\omega_{21}\vec{\imath}
Movimiento relativo {20}
Respecto a la barra el disco efectúa un movimiento de rotación en torno a su eje (la propia barra), por lo que el eje instantáneo de rotación es la recta que pasa por O y por C y la velocidad angular es de la forma

3 Velocidades

Comenzamos anotando lo que sabemos.

Por la condición de rodadura, la velocidad absoluta del punto A es nula

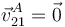
\vec{v}^A_{21}=\vec{0}

El punto C donde se unen solidariamente la barra y el disco, posee velocidad relativa nula

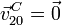
\vec{v}^C_{20}=\vec{0}

También conocemos la velocidad angular del movimiento de arrastre, ya que conocemos el periodo de revolución del disco alrededor del eje vertical

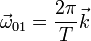
\vec{\omega}_{01}=\frac{2\pi}{T}\vec{k}

También conocemos la posición instantánea de A, B y C. Aplicando semejanza de triángulos tenemos

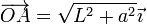
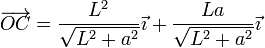
\overrightarrow{OA}=\sqrt{L^2+a^2}\vec{\imath}        \overrightarrow{OC}=\frac{L^2}{\sqrt{L^2+a^2}}\vec{\imath}+\frac{La}{\sqrt{L^2+a^2}}\vec{\imath}        \overrightarrow{OC}=\frac{L^2-a^2}{\sqrt{L^2+a^2}}\vec{\imath}+\frac{2La}{\sqrt{L^2+a^2}}\vec{\imath}

que, para los datos del problema valen, en milímetros:

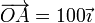
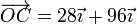
\overrightarrow{OA}=100\vec{\imath}        \overrightarrow{OC}=64\vec{\imath}+48\vec{\imath}        \overrightarrow{OC}=28\vec{\imath}+96\vec{\imath}

por lo que la velocidad de arrastre de C es

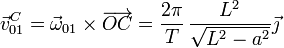
\vec{v}^C_{01}=\vec{\omega}_{01}\times\overrightarrow{OC}=\frac{2\pi}{T}\,\frac{L^2}{\sqrt{L^2-a^2}}\vec{\jmath}

Su velocidad absoluta será la misma por se nula la velocidad relativa

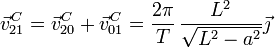
\vec{v}^C_{21}=\vec{v}^C_{20}+\vec{v}^C_{01}=\frac{2\pi}{T}\,\frac{L^2}{\sqrt{L^2-a^2}}\vec{\jmath}

Por otro lado, esta velocidad es igual a

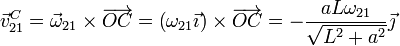
\vec{v}^C_{21}=\vec{\omega}_{21}\times\overrightarrow{OC} = \left(\omega_{21}\vec{\imath}\right)\times\overrightarrow{OC}=-\frac{aL\omega_{21}}{\sqrt{L^2+a^2}}\vec{\jmath}

y de aquí identificamos la velocidad angular absoluta

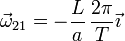
\vec{\omega}_{21}=-\frac{L}{a}\,\frac{2\pi}{T}\vec{\imath}

Restando obtenemos la velocidad angular relativa

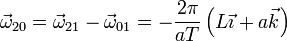
\vec{\omega}_{20}=\vec{\omega}_{21}-\vec{\omega}_{01}=-\frac{2\pi}{aT}\left(L\vec{\imath}+a\vec{k}\right)

Tal como habíamos dicho, esta velocidad angular apunta en la dirección de la barra.

Por otro lado, la velocidad de arrastre del punto A es

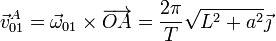
\vec{v}^A_{01}=\vec{\omega}_{01}\times\overrightarrow{OA}=\frac{2\pi}{T}\sqrt{L^2+a^2}\vec{\jmath}

y la relativa será igual y opuesta a esta

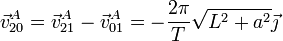
\vec{v}^A_{20}=\vec{v}^A_{21}-\vec{v}^A_{01}=-\frac{2\pi}{T}\sqrt{L^2+a^2}\vec{\jmath}

Las velocidades de arrastre, relativa y absoluta de B se obtienen del mismo modo

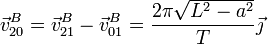
\vec{v}^B_{01}=\vec{\omega}_{01}\times\overrightarrow{OB}=\frac{2\pi(L^2-a^2)}{T\sqrt{L^2+a^2}}\vec{\jmath}        \vec{v}^B_{21}=\vec{\omega}_{21}\times\overrightarrow{OB}=\frac{4\pi L^2}{T\sqrt{L^2+a^2}}\vec{\jmath}        \vec{v}^B_{20}=\vec{v}^B_{21}-\vec{v}^B_{01} = \frac{2\pi\sqrt{L^2-a^2}}{T}\vec{\jmath}

Sustituyendo los valores numéricos obtenemos los siguientes resultados,

Movimiento Arrastre {01} Relativo {20} Absoluto {21}
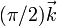
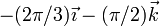
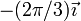
\vec{\omega} (1/s) (\pi/2)\vec{k} -(2\pi/3)\vec{\imath}-(\pi/2)\vec{k} -(2\pi/3)\vec{\imath}
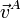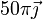
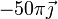
\vec{v}^A (mm/s) 50\pi\vec{\jmath} -50\pi\vec{\jmath} \vec{0}
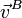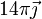
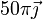
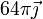
\vec{v}^B (mm/s) 14\pi\vec{\jmath} 50\pi\vec{\jmath} 64\pi\vec{\jmath}
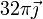
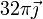
\vec{v}^C (mm/s) 32\pi\vec{\jmath} \vec{0} 32\pi\vec{\jmath}

4 Aceleraciones

En el caso de las aceleraciones sabemos que, por girar uniformemente el disco en torno al eje OZ

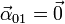
\vec{\alpha}_{01}=\vec{0}

También es nula la aceleración angular relativa

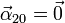
\vec{\alpha}_{20}=\vec{0}

ya que el disco gira uniformemente en el sistema intermedio.

La aceleración angular absoluta, en cambio, no es nula

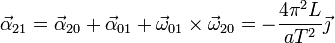
\vec{\alpha}_{21}=\vec{\alpha}_{20}+\vec{\alpha}_{01}+\vec{\omega}_{01}\times\vec{\omega}_{20}=-\frac{4\pi^2 L}{a T^2}\vec{\jmath}

Puesto que conocemos las velocidades y aceleraciones de los tres movimientos y sabemos que existe un punto fijo en los tres movimientos, podemos aplicar en todos los casos, la fórmula general del campo de aceleraciones de un sólido.

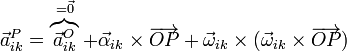
\vec{a}^P_{ik} = \overbrace{\vec{a}^O_{ik}}^{=\vec{0}}+\vec{\alpha}_{ik}\times\overrightarrow{OP}+\vec{\omega}_{ik}\times(\vec{\omega}_{ik}\times\overrightarrow{OP})

Esto nos da los siguientes resultados:

4.1 Movimiento de arrastre

El sólido 0 efectúa una rotación uniforme alrededor del eje OZ por lo que la aceleración de todos los puntos equivale a la de un movimiento circular uniforme: radial hacia adentro de la circunferencia y de módulo igual al cuadrado de la velocidad angular multiplicada por la distancia al eje de giro.

Punto A
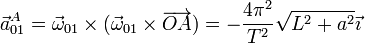
\vec{a}^A_{01}=\vec{\omega}_{01}\times(\vec{\omega}_{01}\times\overrightarrow{OA})=-\frac{4\pi^2}{T^2}\sqrt{L^2+a^2}\vec{\imath}
Punto B
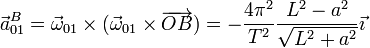
\vec{a}^B_{01}=\vec{\omega}_{01}\times(\vec{\omega}_{01}\times\overrightarrow{OB})=-\frac{4\pi^2}{T^2}\frac{L^2-a^2}{\sqrt{L^2+a^2}}\vec{\imath}
Punto C
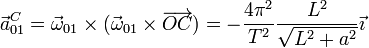
\vec{a}^C_{01}=\vec{\omega}_{01}\times(\vec{\omega}_{01}\times\overrightarrow{OC})=-\frac{4\pi^2}{T^2}\frac{L^2}{\sqrt{L^2+a^2}}\vec{\imath}

4.2 Movimiento relativo

El sólido 2 también efectúa una rotación uniforme, en este caso en torno en torno a la barra. La aceleración de todos los puntos es de nuevo la de un movimiento circular uniforme: radial hacia adentro de la circunferencia y de módulo igual al cuadrado de la velocidad angular multiplicada por la distancia al eje de giro.

Punto A
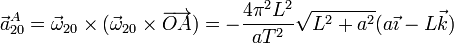
\vec{a}^A_{20}=\vec{\omega}_{20}\times(\vec{\omega}_{20}\times\overrightarrow{OA})=-\frac{4\pi^2L^2}{a T^2}\sqrt{L^2+a^2}(a\vec{\imath}-L\vec{k})
Punto B
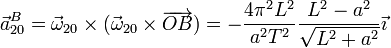
\vec{a}^B_{20}=\vec{\omega}_{20}\times(\vec{\omega}_{20}\times\overrightarrow{OB})=-\frac{4\pi^2L^2}{a^2T^2}\frac{L^2-a^2}{\sqrt{L^2+a^2}}\vec{\imath}
Punto C
\vec{a}^C_{20}=\vec{\omega}_{20}\times(\vec{\omega}_{20}\times\overrightarrow{OC})=\vec{0}
Obtenido de "http://tesla.us.es/wiki/index.php/Rotaci%C3%B3n_de_un_disco_inclinado"

Herramientas:

Herramientas personales
TOOLBOX
LANGUAGES
licencia de Creative Commons
 Aviso legal - Acerca de Laplace