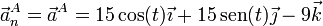4.7. Ejemplo de movimiento de precesión
De Laplace
(→Campo de aceleraciones) |
(→Componentes intrínsecas) |
||
| Línea 49: | Línea 49: | ||
==Componentes intrínsecas== | ==Componentes intrínsecas== | ||
| + | ===Punto A=== | ||
| + | Particularizando para <math>x = y = 0</math>, <math>z=1</math> obtenemos | ||
| + | |||
| + | <center><math>\vec{v}^A = 3\,\mathrm{sen}(t)\vec{\imath}-3\cos(t)\vec{\jmath}</math>{{qquad}}{{qquad}}<math>\vec{a}^A = 15\cos(t)\vec{\imath}+15\,\mathrm{sen}(t)\vec{\jmath}-9\vec{k}</math></center> | ||
| + | |||
| + | Una vez que tenemos los vectores velocidad aceleración podemos hallar las componentes intrínsecas de la aceleración. | ||
| + | |||
| + | ;Aceleración tangencial: Proyectando sobre la velocidad | ||
| + | |||
| + | <center><math>\vec{a}^A_t = \frac{(\vec{a}^A\cdot\vec{v}^A)\vec{v}^A}{(v^A)^2} = \vec{0}</math></center> | ||
| + | |||
| + | ;Aceleración normal: Puesto que la aceleración tangencial es nula, toda la aceleración es normal | ||
| + | |||
| + | <center><math>\vec{a}^A_n = \vec{a}^A = 15\cos(t)\vec{\imath}+15\,\mathrm{sen}(t)\vec{\jmath}-9\vec{k}</math></center> | ||
[[Categoría:Problemas de cinemática del sólido rígido]] | [[Categoría:Problemas de cinemática del sólido rígido]] | ||
Revisión de 22:34 3 ago 2010
Contenido |
1 Enunciado
El movimiento de precesión de una peonza puede describirse como una rotación en torno a un eje instantáneo que a su vez está rotando, manteniéndose fijo el punto de apoyo. Supongamos el caso particular
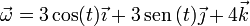
- Determine el campo de velocidades del sólido.
- Determine el campo de aceleraciones del sólido. ¿Es la aceleración de un punto igual a la derivada de la velocidad en ese punto respecto al tiempo?
- Halle, para cada instante las componentes intrínsecas de la aceleración y el radio de curvatura de los puntos

2 Campo de velocidades
Por tratarse de una rotación pura
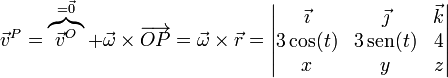
Separando en componentes cartesianas
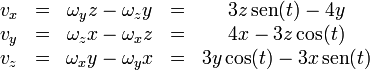
3 Campo de aceleraciones
El campo de aceleraciones tiene la expresión general
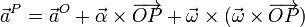
En este caso la aceleración de O es nula, por estar permanentemente en reposo, mientras que la aceleración angular vale
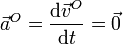
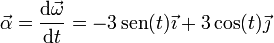
Sustituyendo y separando en componentes cartesianas obtenemos
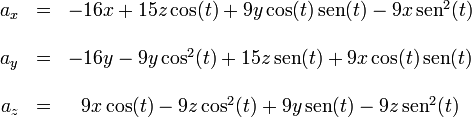
Puede comprobarse de manera inmediata que
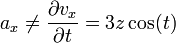
y lo mismo para el resto de las componentes: la aceleración de un punto no es igual a la derivada de la velocidad instantánea de dicho punto respecto al tiempo. La razón es que al tener una velocidad no solo cambia la velocidad porque varía t. También x, y y z varían al desplazarse la partícula y por tanto deben ser incluidas en la derivación respecto al tiempo mediante la regla de la cadena.
4 Componentes intrínsecas
4.1 Punto A
Particularizando para x = y = 0, z = 1 obtenemos
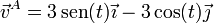
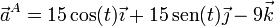
Una vez que tenemos los vectores velocidad aceleración podemos hallar las componentes intrínsecas de la aceleración.
- Aceleración tangencial
- Proyectando sobre la velocidad
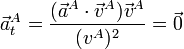
- Aceleración normal
- Puesto que la aceleración tangencial es nula, toda la aceleración es normal