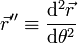Triángulo en movimiento helicoidal
De Laplace
(→Aceleración normal) |
(→Aceleración normal) |
||
| Línea 67: | Línea 67: | ||
<center><math>v^C = \frac{\sqrt{h^2+R^2}}{h}v(t)</math></center> | <center><math>v^C = \frac{\sqrt{h^2+R^2}}{h}v(t)</math></center> | ||
| + | |||
| + | El radio de curvatura de una hélice no es, como pudiera pensarse, igual a R, el radio del cilindro sobre el que se encuentra. Para calcularlo se emplea la fórmula general | ||
| + | |||
| + | <center><math>R_c = \frac{\left|\vec{r}'\right|^3}{\left|\vec{r}'\times\vec{r}''\right|}</math>{{qquad}}{{qquad}}<math>\vec{r}'\equiv \frac{\mathrm{d}\vec{r}}{\mathrm{d}\theta}</math>{{qquad}}{{qquad}}<math>\vec{r}''\equiv \frac{\mathrm{d}^2\vec{r}}{\mathrm{d}\theta^2}</math></center> | ||
==Aceleración y ley horaria== | ==Aceleración y ley horaria== | ||
[[Categoría:Problemas de cinemática del sólido rígido]] | [[Categoría:Problemas de cinemática del sólido rígido]] | ||
Revisión de 18:02 3 ago 2010
Contenido |
1 Enunciado
El triángulo de vértices A, B y C, constituye un sólido rígido en movimiento respecto del sistema de referencia fijo OXYZ. De dicho movimiento se conocen los siguientes datos:
- Los vértices A y B permanecen en todo instante sobre el eje OZ, desplazándose ambos con igual velocidad instantánea:
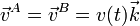 .
.
- El vértice C se mueve describiendo la hélice Γ, que en el sistema OXYZ está descrita por las ecuaciones paramétricas siguientes (donde R y h son constantes conocidas):

- Indique de forma razonada cuál es el eje instantáneo de rotación y mínimo deslizamiento en el movimiento descrito. Determine el vector velocidad angular en términos de los datos expresados en el enunciado.
- Exprese la componente normal de la aceleración del vértice C en un instante cualquiera, en función de los datos del enunciado.
- Para el caso en que v(t) = v0 (cte.), y h = R / 2, calcule la aceleración del vértice C. Determine la ley horaria s = s(t) con que el punto C describe su trayectoria.
2 EIRMD
El eje instantáneo de rotación y mínimo deslizamiento se caracteriza porque en cada uno de sus puntos

Por otro lado, tenemos que, dados dos puntos cualesquiera del sólido
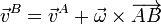
En este caso en concreto tenemos que las velocidades de A y B son iguales por lo que
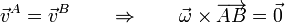
Esto quiere decir que  es paralelo a
es paralelo a 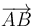 y por tanto
y por tanto
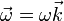
Pero esta misma direccion es la de las velocidades de A y B
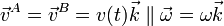
Por tanto el EIRMD no es otro que el el eje que pasa por A y B: el eje Z.
La velocidad de deslizamiento, común a todos los puntos del sólido, será igual a la de A o B
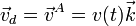
3 Aceleración normal
La aceleración normal de C es igual a
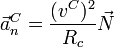
siendo Rc el radio de curvatura de la trayectoria.
De la velocidad de C necesitamos la celeridad, pero solo conocemos la componente vertical que es igual a la velocidad de deslizamiento

Relacionamos ambas cosas observando que
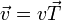
siendo el vector tangente

A partir de las ecuaciones paramétricas de la hélice obtenemos el vector tangente
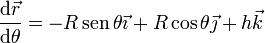
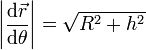
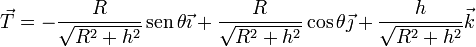
Por tanto la componente vertical de la velocidad de C es

y de aquí obtenemos la celeridad de C

El radio de curvatura de una hélice no es, como pudiera pensarse, igual a R, el radio del cilindro sobre el que se encuentra. Para calcularlo se emplea la fórmula general