Problemas de cinemática del sólido rígido (G.I.T.I.)
De Laplace
(Diferencias entre revisiones)
(→Ejemplo de campo de velocidades) |
(→Ejemplo de campo de velocidades de un sólido) |
||
| Línea 8: | Línea 8: | ||
# Determine la velocidad angular y la velocidad de deslizamiento. | # Determine la velocidad angular y la velocidad de deslizamiento. | ||
# Halle la ecuación del eje instantáneo de rotación y mínimo deslizamiento. | # Halle la ecuación del eje instantáneo de rotación y mínimo deslizamiento. | ||
| + | |||
| + | ==Velocidad de tres puntos de un sólido== | ||
| + | Los vectores de posición y las velocidades de tres puntos de un sólido son, en el SI, | ||
| + | |||
| + | <center><math> | ||
| + | \begin{array}{rclcrcl} | ||
| + | \overrightarrow{OA}&=&\vec{\imath}+\vec{k}&\qquad & | ||
| + | \vec{v}^A=6\vec{\imath}+4\vec{\imath}+a\vec{k}\\ | ||
| + | \overrightarrow{OB}&=&-\vec{\imath}+\vec{\jmath}&\qquad & | ||
| + | \vec{v}^A=b\vec{\imath}+\vec{\imath}-2\vec{k}\\ | ||
| + | \overrightarrow{OA}&=&-\vec{\jmath}-\vec{k}&\qquad & | ||
| + | \vec{v}^A=4\vec{\imath}+c\vec{\jmath}+2\vec{k} | ||
| + | \end{array} | ||
| + | </math></center> | ||
| + | |||
| + | # Halle los valores de <math>a</math>, <math>b</math>, <math>c</math>. | ||
| + | # Halle la velocidad del punto <math>\overrightarrow{OP}=\vec{\imath}-\vec{\jmath}</math>. | ||
| + | # Calcule la velocidad angular y la de deslizamiento | ||
| + | # Determine la posición del eje instantáneo de rotación y mínimo deslizamiento. | ||
[[Categoría:Problemas de cinemática del sólido|0]] | [[Categoría:Problemas de cinemática del sólido|0]] | ||
Revisión de 21:18 2 ago 2010
1 Ejemplo de campo de velocidades de un sólido
Un campo de velocidades de un sistema de partículas tiene la expresión, en el SI,
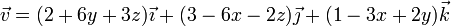
- Pruebe que corresponde al movimiento de un sólido rígido.
- Determine la velocidad angular y la velocidad de deslizamiento.
- Halle la ecuación del eje instantáneo de rotación y mínimo deslizamiento.
2 Velocidad de tres puntos de un sólido
Los vectores de posición y las velocidades de tres puntos de un sólido son, en el SI,
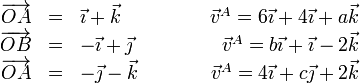
- Halle los valores de a, b, c.
- Halle la velocidad del punto
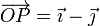 .
.
- Calcule la velocidad angular y la de deslizamiento
- Determine la posición del eje instantáneo de rotación y mínimo deslizamiento.





