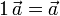Vectores libres
De Laplace
(→Definición geométrica de vector. Clasificación) |
(→Vectores libres. Suma y producto por un escalar) |
||
| Línea 55: | Línea 55: | ||
;Distributiva respecto a la suma de vectores: | ;Distributiva respecto a la suma de vectores: | ||
<center><math>\lambda\,(\vec{a}+\vec{b})=\lambda\,\vec{a}+\lambda\,\vec{b}</math></center> | <center><math>\lambda\,(\vec{a}+\vec{b})=\lambda\,\vec{a}+\lambda\,\vec{b}</math></center> | ||
| - | + | ; Distributiva respecto a la suma de escalares: | |
| - | + | <center><math>(\lambda+\mu)\,\vec{a}=\lambda\,\vec{a}+\mu\,\vec{a}</math></center> | |
| - | + | ;Existencia de escalar unidad: | |
| - | + | <center><math>1\,\vec{a}=\vec{a}</math></center> | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
[[Categoría:Física I (G.I.T.I.)]] | [[Categoría:Física I (G.I.T.I.)]] | ||
Revisión de 11:51 19 jul 2010
1 Magnitudes escalares y vectoriales
Una magnitud física es cualquier propiedad física susceptible de ser medida. Ejemplos: el tiempo (t), la velocidad
(
), la masa (m), la temperatura (T), el campo eléctrico (
).
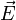Las magnitudes físicas se pueden clasificar en:
- Magnitudes escalares
- son aquéllas que quedan completamente determinadas mediante el conocimiento de su valor expresado mediante una cantidad (un número real) seguida de una unidad (a excepción de las adimensionales). Ejemplos: el tiempo (t), la masa (m), la temperatura (T), la carga eléctrica (q), el coeficiente de rozamiento (μ).
- Magnitudes vectoriales
- son aquéllas que no quedan completamente determinadas por su valor (cantidad y unidad), sino que requieren además el conocimiento de la dirección y el sentido de su actuación, e incluso en algunos casos el conocimiento de su recta soporte o de su punto de aplicación. Ejemplos: la velocidad (), la aceleración (
), la fuerza (
), el campo eléctrico ().
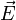- Magnitudes tensoriales
- generalizan el concepto de magnitud vectorial. Mientras las vectoriales pueden ser representadas por una matriz 3×1, las tensoriales requieren matrices 3×3 o incluso entes de mayores dimenriones.
2 Definición geométrica de vector. Clasificación
El concepto de vector es un concepto matemático con interés físico, ya que permite representar o describir las magnitudes vectoriales, así como operar con ellas.
Un vector geométrico es un segmento orientado dotado de los siguientes elementos:
- Módulo
- es su longitud, proporcional al valor de la magnitud física.
- Dirección
- es la dirección de su recta soporte
- Sentido
- es la orientación del segmento, indicada mediante una flecha y que permite definir cuál es su origen y cuál su extremo
- Recta soporte
- es la recta a la que pertenece el segmento
- Punto de aplicación
- es el origen del segmento.
Los vectores geométricos se pueden clasificar en:
- Vectores libres
- son los que quedan definidos mediante su módulo, dirección y sentido. Por tanto, son invariantes ante traslaciones en el espacio. Ejemplo: la resultante de todas las fuerzas que actúan sobre un sólido rígido.
- Vectores deslizantes
- son los que quedan definidos mediante su módulo, dirección, sentido y recta soporte. Por tanto, son invariantes ante deslizamientos a lo largo de su recta soporte. Ejemplos: la velocidad angular, la fuerza que actúa sobre un sólido rígido.
- Vectores ligados
- son los que quedan definidos mediante su módulo, dirección, sentido y punto de aplicación. No existe ningún movimiento que los deje invariantes. Ejemplos: la velocidad, el momento de una fuerza respecto a un punto, el campo eléctrico.
En principio, cada magnitud física vectorial, según su naturaleza, puede ser representada por una de estas tres clases de vectores. Sin embargo, en ocasiones, es la naturaleza del problema físico concreto la que determina que una misma magnitud se describa mediante una u otra clase de vectores. Así, por ejemplo, una fuerza se comporta como un vector deslizante cuando actúa sobre un sólido rígido, y como un vector ligado cuando lo hace sobre un sólido deformable.
3 Vectores libres. Suma y producto por un escalar
Los vectores libres admiten la definición de las operaciones suma y producto por un escalar con una serie de propiedades algebraicas (definición algebraica de vector). No obstante, el primer requisito para poder operar con vectores libres ha de ser la definición de una relación de equivalencia.
La relación de equivalencia entre vectores libres está implícita en la propia definición de éstos, de tal modo que diremos que dos vectores libres son equivalentes (y escribiremos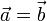 
) cuando tengan respectivamente iguales sus módulos, sus direcciones y sus sentidos (podrán tener diferentes, por tanto, sus rectas soporte y sus puntos de aplicación).
La suma de vectores libres,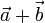 
, se define mediante las conocidas como regla del paralelogramo o
regla del triángulo, y presenta las siguientes propiedades algebraicas:
- Conmutativa
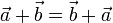
- Asociativa
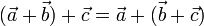
- Existencia de elemento neutro
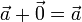
- Existencia de elemento opuesto
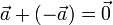
La operación suma, junto a la existencia de elemento opuesto, permite definir la resta o diferencia de vectores:
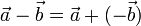
El producto de un vector libre, , por un escalar, λ (número real), se define como un nuevo vector libre,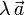 
, cuyo módulo es igual al producto del escalar (en valor absoluto) por el módulo del vector original, cuya dirección es la misma que la del vector original, y cuyo sentido es el mismo o el opuesto al del vector original según el escalar sea positivo o negativo, respectivamente. Esta operación presenta las siguientes propiedades algebraicas:
- Asociativa respecto al producto por escalar
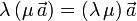
- Distributiva respecto a la suma de vectores
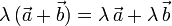
- Distributiva respecto a la suma de escalares
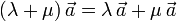
- Existencia de escalar unidad
