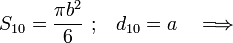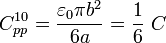Un disco y dos semidiscos paralelos
De Laplace
(→Capacidades eléctricas de los condensadores) |
(→Capacidades eléctricas de los condensadores) |
||
| Línea 10: | Línea 10: | ||
Supongamos que el disco y los semidiscos conductores almacenan sendos valores de carga eléctrica  ''Q'' <sub>0</sub>, ''Q'' <sub>1</sub> y ''Q'' <sub>2</sub>, hallándose en equilibrio electrostático. Cada conductor constituirá una superficie equiescalar para el potencial electrostático  <math>\ \phi (\mathbf{r})</math>, que presentará valores  ''V''<sub>0</sub>, ''V''<sub>1</sub> y ''V''<sub>2</sub>, medidos respecto del origen de potencial que consideraremos situado en el infinito. En general, estos valores van a ser distintos de manera que entre cada par de conductores, así como entre cada uno de ellos y el infinito, hay una diferencia de potencial que se traduce en la existencia de un gradiente y, por tanto, de un campo eléctrico. | Supongamos que el disco y los semidiscos conductores almacenan sendos valores de carga eléctrica  ''Q'' <sub>0</sub>, ''Q'' <sub>1</sub> y ''Q'' <sub>2</sub>, hallándose en equilibrio electrostático. Cada conductor constituirá una superficie equiescalar para el potencial electrostático  <math>\ \phi (\mathbf{r})</math>, que presentará valores  ''V''<sub>0</sub>, ''V''<sub>1</sub> y ''V''<sub>2</sub>, medidos respecto del origen de potencial que consideraremos situado en el infinito. En general, estos valores van a ser distintos de manera que entre cada par de conductores, así como entre cada uno de ellos y el infinito, hay una diferencia de potencial que se traduce en la existencia de un gradiente y, por tanto, de un campo eléctrico. | ||
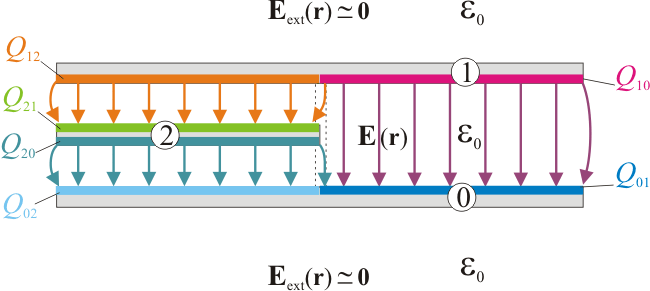
| - | [[Archivo:discoysemidiscos2.gif|left]]En el enunciado se indica que la distancia de separación ''a'' entre disco y semidisco exterior (conductores “0” y “1”, respectivamente) es mucho menor que el tamaño de los conductores (<math>a\ll b</math>). Esto permite realizar en el modelo una serie de simplificaciones que llevan a la obtención de una solución analítica sencilla para el problema del potencial. Como es bien sabido, ésta no va a ser la solución exacta, aunque los valores que proporciona para las diferentes magnitudes eléctricas pueden considerarse suficientemente precisos. En primer lugar se tendrá que el gradiente del potencial,  <math>\nabla \phi (\mathbf{r}</math>, en la región del espacio comprendida entre los conductores y el infinito va a tener un valor despreciable frente al que presentará en los puntos que se hallan entre los conductores; es decir, cuando éstos se hallan cargados eléctricamente y en equilibrio electrostático, el campo eléctrico en el exterior del sistema es prácticamente nulo si se compara con el que hay entre los conductores, pues  <math>\nabla \phi (\mathbf{r})=-\mathbf{E}(\mathbf{r})</math>. En consecuencia, la carga eléctrica en los conductores “1” y “0” se distribuirá exclusivamente en sus caras interiores, mientras que en el “2” lo hará en ambas caras, pues cada una de ellas se encuentra enfrentada a otro conductor del sistema. De esta forma, podemos expresar la cantidad de carga eléctrica en cada conductor de la siguiente manera: | + | [[Archivo:discoysemidiscos2.gif|left]] |
| + | |||
| + | En el enunciado se indica que la distancia de separación ''a'' entre disco y semidisco exterior (conductores “0” y “1”, respectivamente) es mucho menor que el tamaño de los conductores (<math>a\ll b</math>). Esto permite realizar en el modelo una serie de simplificaciones que llevan a la obtención de una solución analítica sencilla para el problema del potencial. Como es bien sabido, ésta no va a ser la solución exacta, aunque los valores que proporciona para las diferentes magnitudes eléctricas pueden considerarse suficientemente precisos. En primer lugar se tendrá que el gradiente del potencial,  <math>\nabla \phi (\mathbf{r}</math>, en la región del espacio comprendida entre los conductores y el infinito va a tener un valor despreciable frente al que presentará en los puntos que se hallan entre los conductores; es decir, cuando éstos se hallan cargados eléctricamente y en equilibrio electrostático, el campo eléctrico en el exterior del sistema es prácticamente nulo si se compara con el que hay entre los conductores, pues  <math>\nabla \phi (\mathbf{r})=-\mathbf{E}(\mathbf{r})</math>. En consecuencia, la carga eléctrica en los conductores “1” y “0” se distribuirá exclusivamente en sus caras interiores, mientras que en el “2” lo hará en ambas caras, pues cada una de ellas se encuentra enfrentada a otro conductor del sistema. De esta forma, podemos expresar la cantidad de carga eléctrica en cada conductor de la siguiente manera: | ||
<center><math>Q_0=Q_{01}+Q_{02}\ \mathrm{;}\qquad Q_1=Q_{10}+Q_{12}\ \mathrm{;}\qquad Q_2=Q_{20}+Q_{21}</math></center> | <center><math>Q_0=Q_{01}+Q_{02}\ \mathrm{;}\qquad Q_1=Q_{10}+Q_{12}\ \mathrm{;}\qquad Q_2=Q_{20}+Q_{21}</math></center> | ||
Revisión de 21:06 13 jul 2010
Contenido |
1 Enunciado
Un disco y un semidisco, ambos conductores y de igual radio b –que denominaremos conductores “0” y “1”, respectivamente– se hallan en sendos planos paralelos separados una distancia a. Un segundo semidisco –conductor “2”–, también de radio b se encuentra entre los conductores anteriores, a igual distancia a/2 de éstos. Los semidiscos no están alineados, sino que sus diámetros forman un ángulo α=60º (véase la figura). Las dimensiones son tales que b es mucho mayor que a de manera que, cuando el sistema se carga eléctricamente, las superficies conductoras enfrentadas pueden considerarse en influencia total, despreciándose los efectos de borde.- Teniendo en cuenta esta aproximación, determine las capacidades eléctricas de los distintos condensadores que forman el sistema de conductores descrito.
- Tomando el disco completo como conductor de referencia (siempre conectado a tierra), obtenga el circuito equivalente y calcule la matriz de coeficientes de capacidad e inducción eléctrica del sistema.
- Con el conductor “0” conectado a tierra y el “2” descargado y aislado, se conecta el conductor “1” a una fuente de potencial V0. Calcule la carga eléctrica en el conductor “1” y el potencial en el conductor “2”.
- Halle la energía electrostática del sistema en la configuración anterior.
2 Capacidades eléctricas de los condensadores
Supongamos que el disco y los semidiscos conductores almacenan sendos valores de carga eléctrica Q 0, Q 1 y Q 2, hallándose en equilibrio electrostático. Cada conductor constituirá una superficie equiescalar para el potencial electrostático 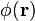 , que presentará valores V0, V1 y V2, medidos respecto del origen de potencial que consideraremos situado en el infinito. En general, estos valores van a ser distintos de manera que entre cada par de conductores, así como entre cada uno de ellos y el infinito, hay una diferencia de potencial que se traduce en la existencia de un gradiente y, por tanto, de un campo eléctrico.
, que presentará valores V0, V1 y V2, medidos respecto del origen de potencial que consideraremos situado en el infinito. En general, estos valores van a ser distintos de manera que entre cada par de conductores, así como entre cada uno de ellos y el infinito, hay una diferencia de potencial que se traduce en la existencia de un gradiente y, por tanto, de un campo eléctrico.
En el enunciado se indica que la distancia de separación a entre disco y semidisco exterior (conductores “0” y “1”, respectivamente) es mucho menor que el tamaño de los conductores (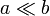 ). Esto permite realizar en el modelo una serie de simplificaciones que llevan a la obtención de una solución analítica sencilla para el problema del potencial. Como es bien sabido, ésta no va a ser la solución exacta, aunque los valores que proporciona para las diferentes magnitudes eléctricas pueden considerarse suficientemente precisos. En primer lugar se tendrá que el gradiente del potencial,
). Esto permite realizar en el modelo una serie de simplificaciones que llevan a la obtención de una solución analítica sencilla para el problema del potencial. Como es bien sabido, ésta no va a ser la solución exacta, aunque los valores que proporciona para las diferentes magnitudes eléctricas pueden considerarse suficientemente precisos. En primer lugar se tendrá que el gradiente del potencial, 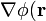 , en la región del espacio comprendida entre los conductores y el infinito va a tener un valor despreciable frente al que presentará en los puntos que se hallan entre los conductores; es decir, cuando éstos se hallan cargados eléctricamente y en equilibrio electrostático, el campo eléctrico en el exterior del sistema es prácticamente nulo si se compara con el que hay entre los conductores, pues
, en la región del espacio comprendida entre los conductores y el infinito va a tener un valor despreciable frente al que presentará en los puntos que se hallan entre los conductores; es decir, cuando éstos se hallan cargados eléctricamente y en equilibrio electrostático, el campo eléctrico en el exterior del sistema es prácticamente nulo si se compara con el que hay entre los conductores, pues 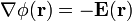 . En consecuencia, la carga eléctrica en los conductores “1” y “0” se distribuirá exclusivamente en sus caras interiores, mientras que en el “2” lo hará en ambas caras, pues cada una de ellas se encuentra enfrentada a otro conductor del sistema. De esta forma, podemos expresar la cantidad de carga eléctrica en cada conductor de la siguiente manera:
. En consecuencia, la carga eléctrica en los conductores “1” y “0” se distribuirá exclusivamente en sus caras interiores, mientras que en el “2” lo hará en ambas caras, pues cada una de ellas se encuentra enfrentada a otro conductor del sistema. De esta forma, podemos expresar la cantidad de carga eléctrica en cada conductor de la siguiente manera:
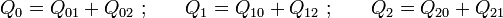
donde Q ij es la cantidad parcial de carga eléctrica distribuida en el sector del conductor “i” que se encuentra directamente enfrentada al conductor “j”. Y también como consecuencia de la condición 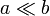 , podemos considerar que los sectores enfrentados de cada par de conductores están en influencia total, almacenando cantidades opuestas de carga eléctrica y formando sendos condensadores de placas plano paralelas, caracterizados cada uno de ellos por su correspondiente capacidad eléctrica, thinsp;Cppij, que establece la relación entre la carga almacenada y la diferencia de potencial entre las placas:
, podemos considerar que los sectores enfrentados de cada par de conductores están en influencia total, almacenando cantidades opuestas de carga eléctrica y formando sendos condensadores de placas plano paralelas, caracterizados cada uno de ellos por su correspondiente capacidad eléctrica, thinsp;Cppij, que establece la relación entre la carga almacenada y la diferencia de potencial entre las placas:
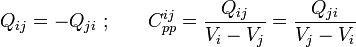
Como sabemos, la capacidad eléctrica es una magnitud que depende de la geometría del condensador. En el caso que estamos analizando, la proximidad entre las láminas conductoras en relación con su tamaño permite despreciar los efectos de borde, de manera que el campo eléctrico entre cada par de placas va a ser perpendicular a éstas y de módulo constante en prácticamente todos los puntos situados entre ellas. En consecuencia, la cantidad parcial de carga eléctrica Q ij se distribuirá uniformemente en el sector del conductor “i” enfrentado al “j” y el correspondiente valor de capacidad se corresponderá con el del modelo ideal de condensador de placas plano paralelas,
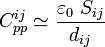
siendo Sij el área de los sectores en los conductores “i” y “j” que se encuentran en influencia total, y dij la distancia que los separa.
En el sistema bajo estudio los conductores “0” y “2” tienen enfrentados el sector correspondiente a un semidisco de radio b y están separados una distancia a/2:

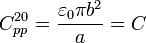
Los semidiscos conductores “1” y “2” están separados esa misma distancia y se encuentran girados un ángulo π/3, por lo que se enfrentan en un sector circular correspondiente a 2/3 de un semidisco (ó 1/3 de disco); se tendrá, por tanto,

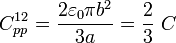
Finalmente, los conductores “1” y “0” se enfrentan en un sector circular correspondiente a 1/3 de semidisco de radio b (o lo que es lo mismo, 1/6 de disco), separados una distancia a; entonces,