Problemas de cinemática del punto material (G.I.T.I.)
De Laplace
(Diferencias entre revisiones)
(→Movimiento helicoidal) |
(→Espiral logarítmica) |
||
| Línea 32: | Línea 32: | ||
# Halle el vector aceleración y sus componentes intrínsecas en cada punto de la trayectoria. | # Halle el vector aceleración y sus componentes intrínsecas en cada punto de la trayectoria. | ||
# Determine la posición de los centros de curvatura de este movimiento. | # Determine la posición de los centros de curvatura de este movimiento. | ||
| + | |||
| + | ==[[Evoluta de una circunferencia]]== | ||
| + | La evoluta de una circunferencia es la curva que se obtiene cuando se desenrolla un hilo tenso de un carrete circular. Suponga que se tiene una bobina que se va desenrollando a ritmo constante, de forma que el punto de contacto del hilo con el carrete forma un ángulo <math>\theta=\omega t</math> con el punto inicial. Una partícula material se encuentra en el extremo del hilo | ||
| + | |||
| + | |||
| + | |||
| + | |||
[[Categoría:Problemas de cinemática de la partícula|0]] | [[Categoría:Problemas de cinemática de la partícula|0]] | ||
[[Categoría:Cinemática de la partícula]] | [[Categoría:Cinemática de la partícula]] | ||
Revisión de 10:38 24 jun 2010
Contenido |
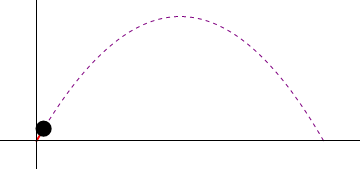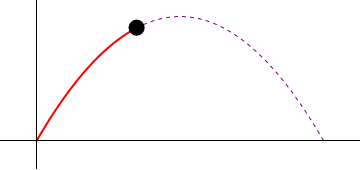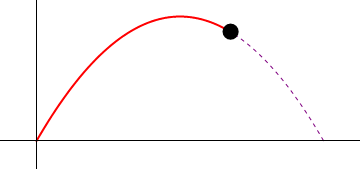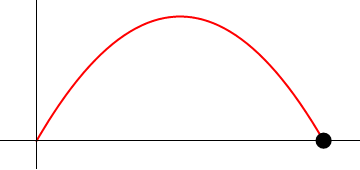
1 Cinemática del tiro parabólico
Supóngase el movimiento de un proyectil, dado en coordenadas cartesianas por
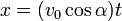
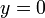
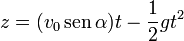
- Determine el vector de posición, la velocidad y la aceleración en cada instante.
- Calcule la celeridad y el vector tangente en el instante inicial, en el instante en que se encuentra a mayor altura y en el momento en que vuelve a impactar con el suelo.
- Halle la aceleración tangencial y la aceleración normal, así como el vector unitario normal en los tres instantes anteriores.
- Calcule el radio de curvatura y el centro de curvatura en los mismos tres instantes.
2 Movimiento helicoidal
Una partícula recorre la hélice
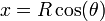
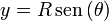
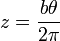
según la ley horaria
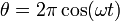
3 Espiral logarítmica
Una partícula recorre la espiral logarítmica de ecuación
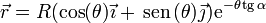
donde R y α son constantes. El movimiento es uniforme a lo largo de la curva, con celeridad constante v0. En el instante inicial la partícula se encuentra en θ = 0
- Determine la ley horaria θ = θ(t).
- Calcule el tiempo que tarda en llegar a
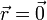. ¿Cuántas vueltas da para ello?
- Halle el vector aceleración y sus componentes intrínsecas en cada punto de la trayectoria.
- Determine la posición de los centros de curvatura de este movimiento.
4 Evoluta de una circunferencia
La evoluta de una circunferencia es la curva que se obtiene cuando se desenrolla un hilo tenso de un carrete circular. Suponga que se tiene una bobina que se va desenrollando a ritmo constante, de forma que el punto de contacto del hilo con el carrete forma un ángulo θ = ωt con el punto inicial. Una partícula material se encuentra en el extremo del hilo
