Problemas de cinemática del punto material (G.I.T.I.)

(Diferencias entre revisiones)

Revisión de 11:30 23 jun 2010

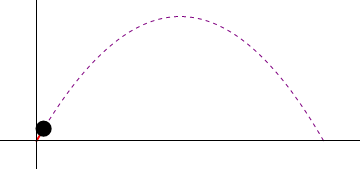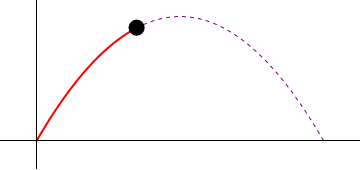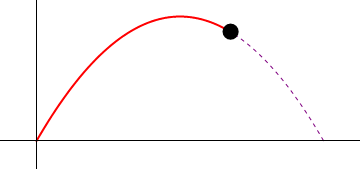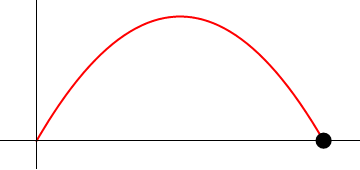
Supóngase el movimiento de un proyectil, dado en coordenadas cartesianas por

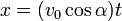
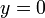
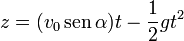
$x=(v_0\cos\alpha)t\,$ $y=0\,$ $z=(v_0\,\mathrm{sen}\,\alpha)t-\frac{1}{2}gt^2$

Determine el vector de posición, la velocidad y la aceleración en cada instante.
Calcule la celeridad y el vector tangente en el instante inicial, en el instante en que se encuentra a mayor altura y en el momento en que vuelve a impactar con el suelo.
Halle la aceleración tangencial y la aceleración normal, así como el vector unitario normal en los tres instantes anteriores.
Calcule el radio de curvatura y el centro de curvatura en los mismos tres instantes.

Una partícula recorre la hélice

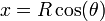
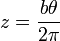
$x = R\cos(\theta)\,$ $y = R\,\mathrm{sen}\,\theta$ {qquad}} $z=\frac{b\theta}{2\pi}$

según la ley horaria

$\theta = 2\pi\cos(\omega t)\,$

@@ Línea 15: / Línea 15: @@
 Una partícula recorre la hélice
-<center><math>x = R\cos(\theta)\,</math>{{qquad}<math>}y = R\,\mathrm{sen}\,\theta</math>{qquad}}{{qquad}}<math>z=\frac{b\theta}{2\pi}</math></center>
+<center><math>x = R\cos(\theta)\,</math>{{qquad}}<math>y = R\,\mathrm{sen}\,\theta</math>{qquad}}{{qquad}}<math>z=\frac{b\theta}{2\pi}</math></center>
 según la ley horaria