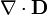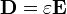Esfera conductora sumergida en dieléctrico
De Laplace
(Diferencias entre revisiones)
(→Potencial y campo eléctrico) |
(→Ecuación para el potencial) |
||
| Línea 13: | Línea 13: | ||
==Potencial y campo eléctrico== | ==Potencial y campo eléctrico== | ||
===Ecuación para el potencial=== | ===Ecuación para el potencial=== | ||
| + | Las ecuaciones que determinan los campos en presencia de dieléctricos lineales son | ||
| + | |||
| + | <center><math>\nabla\cdot\mathbf{D}</math>{{qquad}}{{qquad}}<math>\nabla\times\mathbf{E}=\mathbf{0}</math>{{qquad}}{{qquad}}<math>\mathbf{D}=\varepsilon \mathbf{E}</math></center> | ||
| + | |||
===Potencial eléctrico=== | ===Potencial eléctrico=== | ||
===Campo eléctrico=== | ===Campo eléctrico=== | ||
Revisión de 17:00 14 jun 2010
Contenido |
1 Enunciado
Una esfera conductora de radio a se encuentra conectada a una fuente de tensión de valor V0. La esfera se encuentra semisumergida en un líquido dieléctrico ideal de permitividad  .
.
- Obtenga la expresión del potencial electrostático y del campo eléctrico en todo el espacio. Suponga que el potencial sólo depende de la distancia al centro de la esfera.
- Obtenga la expresión del vector desplazamiento en todo el espacio. Calcule la cantidad de carga libre en la esfera conductora.
- Determine las distribuciones de carga libre y de polarización que hay en el sistema descrito.
- Calcule la energía electrostática almacenada en el sistema.
- Si, sin desconectar la fuente, se retira el líquido dieléctrico, ¿cuánto cambia la energía almacenada? ¿Cuánto trabajo realiza el generador?
2 Potencial y campo eléctrico
2.1 Ecuación para el potencial
Las ecuaciones que determinan los campos en presencia de dieléctricos lineales son