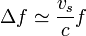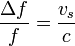Entrar Página Discusión Historial Go to the site toolbox

Efecto Doppler

De Laplace

(Diferencias entre revisiones)
(→Caso de que los dos estén en movimiento)
(→Caso de que los dos estén en movimiento)
Línea 64: Línea 64:
<center><math>T' = \frac{cT_i}{c-v_o} =\frac{c}{c-v_o}\left(1-\frac{v_s}{c}\right)T = \frac{c-v_s}{c-v_o}T</math>{{tose}} <math>f' = \frac{c-v_o}{c-v_s}f</math></center>
<center><math>T' = \frac{cT_i}{c-v_o} =\frac{c}{c-v_o}\left(1-\frac{v_s}{c}\right)T = \frac{c-v_s}{c-v_o}T</math>{{tose}} <math>f' = \frac{c-v_o}{c-v_s}f</math></center>
 +
 +
<center>[[Imagen:vspvop.gif]]</center>
 +
 +
Sin recurrir al observador intermedio, empleamos la construcción indicada en la figura y vemos que se cumple la relación
 +
 +
<center><math>c(T-T') + v_oT' = v_sT\,</math>{{tose}} <math>T' = \frac{c-v_s}{c-v_o}T</math>{{tose}}<math>f' = \frac{c-v_o}{c-v_s}f</math></center>
==Corrimiento en la frecuencia==
==Corrimiento en la frecuencia==

Revisión de 14:16 18 mar 2010

Contenido

1 Introducción

2 Efecto Doppler para ondas sonoras

2.1 Caso de un observador en movimiento

Consideremos en primer lugar el caso de una fuente en reposo respecto al medio circundante (el aire). Esta fuente emite ondas de frecuencia f, o equivalentemente, emite frentes de onda espaciadas un periodo T = 1 / f. Estas ondas se propagan el el aire radialmente con velocidad c. La distancia entre crestas sucesivas, en el sistema de la fuente, será λ = cT.

Queremos determinar la frecuencia que mide un observador que se acerca o se aleja radialmente de la fuente. Al estar la fuente, el observador y la dirección de propagación alineadas, podemos usar cantidades escalares, en lugar de vectoriales, y llamar v0 a la velocidad de este observador.

Tomaremos vo > 0 si el observador se aleja de la fuente y negativa si se acerca a ella.

Cuando el observador se aleja de la fuente, los frentes llegan a él con un intervalo mayor que con el que fueron emitidos, ya que cada frente debe recorrer una distancia adicional para alcanzar al observador, la que éste ha recorrido en el tiempo intermedio.

Supongamos que una cresta llega al observador en un instante t. La siguiente llegará en un instante t + T', en este tiempo el observador ha recorrido una distancia

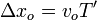
\Delta x_o = v_oT'\,

Este segundo frente llegó a la posición original del observador un tiempo T tras el anterior. Para alcanzar al observador debe recorrer la distancia que éste ha avanzado y para ello empleará un tiempo T' − T. Por tanto

Δxo = c(T' − T) = voT'

Despejando

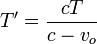
T' = \frac{cT}{c-v_o}

y la frecuencia medida por el observador es

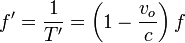
f' = \frac{1}{T'}=\left(1-\frac{v_o}{c}\right)f

El observador mide una frecuencia menor cuando el observador se aleja, y una mayor cuando se acerca.

Podemos representar este resultado gráficamente. Trazando una gráfica en la que el eje de abscisas es la distancia a la fuente y el de ordenadas el tiempo, la fuente estacionaria aparece como una línea vertical. Los frentes de onda son líneas que se alejan de la fuente en ambos sentidos, con una pendiente T / λ = 1 / c. El observador que se aleja de la fuente será una línea oblicua, con una pendiente 1 / vo, mayor (esto es, más vertical) que la de los frentes de onda (si no, éstos no le alcanzarían). Considerando el triángulo señalado en la figura, obtenemos el resultado anterior.

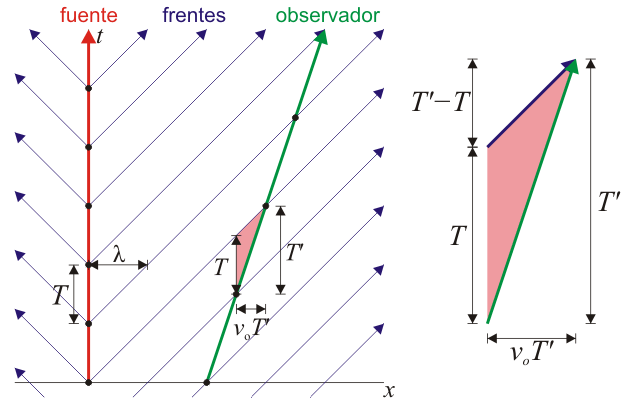
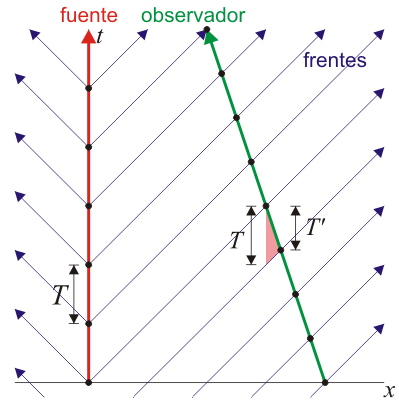
Imagen:Dvs0vop.gif        Imagen:Dvs0von.gif

El mismo resultado se obtiene en el caso en que el observador se acerque a la fuente, solo que en ese caso el observador va al encuentro de los frentes de onda, y por tanto mide un periodo menor, y una frecuencia mayor.

En este caso tendríamos, de acuerdo con la figura

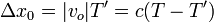
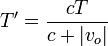
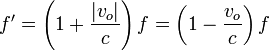
\Delta x_0 = |v_o|T' = c(T-T')\,   \Rightarrow    T' = \frac{c T}{c+|v_o|}   \Rightarrow    f'=\left(1+\frac{|v_o|}{c}\right)f = \left(1-\frac{v_o}{c}\right)f

Matemáticamente la fórmula es la misma que antes, cuando se tiene en cuenta el signo de la velocidad del observador.

2.2 Caso de una fuente en movimiento

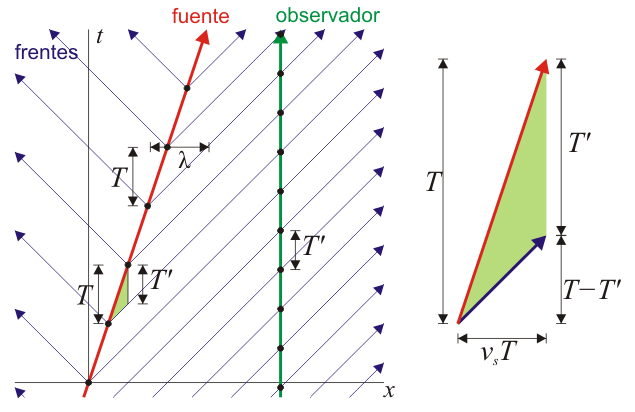
Supongamos ahora el caso de una fuente en movimiento (a una velocidad vs inferior a la del sonido, c) y un observador en reposo.

En este caso los frentes de onda se van emitiendo desde un punto que va avanzando, y por tanto se acumulan por la “proa”, mientras se enrarecen por la “popa”. El resultado es que un observador estacionario situado delante del emisor, mide una frecuencia de recepción mayor que la de emisión, mientras que uno situado por detrás mide una frecuencia mayor.

Supongamos que el emisor avanza hacia el receptor con velocidad vs positiva, de forma que los frentes de onda se emiten en intervalos de T segundos y por tanto desde puntos espaciados vsT metros. Para llegar al receptor el primer frente debe recorrer una distancia X a una velocidad c, mientras que el segundo sólo recorrerá X − vsT (pero fue emitido un tiempo T más tarde). Empleando la construcción indicada en la figura tenemos que

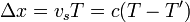
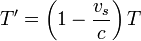
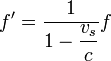
\Delta x = v_sT = c(T-T')\,   \Rightarrow   T'=\left(1-\frac{v_s}{c}\right)T   \Rightarrow   f'=\frac{1}{1-\displaystyle{\frac{v_s}{c}}}f
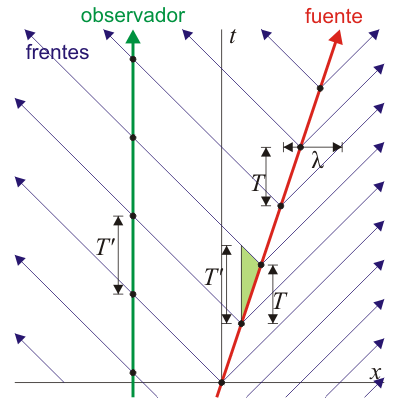
Imagen:Dvspvo0.gif    Imagen:Dvsnvo0.gif

El mismo resultado se obtiene si el observador se encuentra a popa del emisor. En este caso el cálculo es

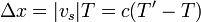
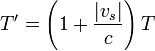
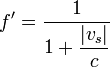
\Delta x = |v_s| T = c(T'-T) \,   \Rightarrow   T'=\left(1+\frac{|v_s|}{c}\right)T   \Rightarrow   f'=\frac{1}{1+\displaystyle{\frac{|v_s|}{c}}}

que coincide con el anterior si se considera que la velocidad es negativa cuando el emisor se aleja del receptor.

2.3 Caso de que los dos estén en movimiento

Cuando tanto la fuente como el receptor se encuentran en movimiento respecto al medio, el efecto Dopler resultante será una combinación de los dos anteriores. Podemos realizar el cálculo relacionando directamente lo que mide el emisor con lo que mide el receptor, o empleando un observador intermedio ficticio en reposo respecto al aire. Este observador se limitaría a reemitir las señales que le llegan.

Empleando al observador intermedio, que mide un periodo Ti resulta un efecto Doppler que es el producto de los otros dos por separado.

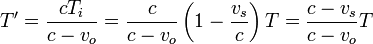
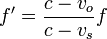
T' = \frac{cT_i}{c-v_o} =\frac{c}{c-v_o}\left(1-\frac{v_s}{c}\right)T = \frac{c-v_s}{c-v_o}T   \Rightarrow    f' = \frac{c-v_o}{c-v_s}f
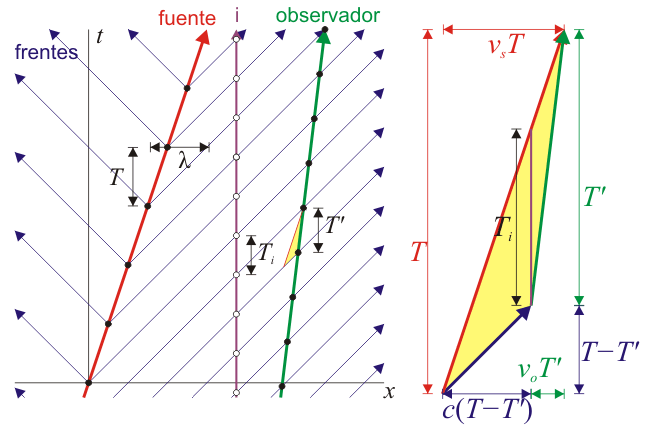
Imagen:vspvop.gif

Sin recurrir al observador intermedio, empleamos la construcción indicada en la figura y vemos que se cumple la relación

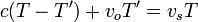
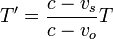
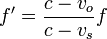
c(T-T') + v_oT' = v_sT\,   \Rightarrow    T' = \frac{c-v_s}{c-v_o}T   \Rightarrow   f' = \frac{c-v_o}{c-v_s}f

3 Corrimiento en la frecuencia

A menudo el efecto Doppler es solo una pequeña corrección respecto a la frecuencia emitida, debido a que la velocidad de la fuente y del observador es pequeña comparada con la velocidad de la onda en el medio. En este caso, más informativo que dar la frecuencia absoluta, interesa dar el corrimiento en la frecuencia que es la diferencia entre la frecuencia medida por el observador y la emitida por la fuente

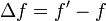
\Delta f = f'-f\,

También se define el corrimiento relativo como el cociente entre esta cantidad y la frecuencia emitida

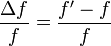
\frac{\Delta f}{f}=\frac{f'-f}{f}

3.1 Caso del observador en movimiento

Sustituyendo la frecuencia medida por el observador

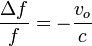
\Delta f = \left(1-\frac{v_o}{c}\right)f - f = -\frac{v_o}{c}f   \Rightarrow   \frac{\Delta f}{f}=-\frac{v_o}{c}

Este corrimiento es negativo (“hacia el rojo”) cuando el observador se aleja de la fuente (vo > 0) y positivo (“hacia el violeta”) cuando el observador se acerca a ella.

3.2 Caso de la fuente en movimiento

Si es la fuente la que se mueve, el corrimiento en la frecuencia es exactamente

\Delta f =\frac{f}{1-\displaystyle\frac{v_s}{c}} - f = \frac{\displaystyle\frac{v_s}{c}}{1-\displaystyle\frac{v_s}{c}}f

Si la velocidad de la fuente es muy pequeña compara con la de la onda 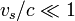v_s/c\ll 1 y podemos despreciar el segundo término del denominador, quedando el corrimiento en la frecuencia

\Delta f\simeq \frac{v_s}{c}f   \Rightarrow   \frac{\Delta f}{f} = \frac{v_s}{c}

4 Efecto Doppler para la radiación electromagnética

4.1 Límite clásico

4.2 Expresión relativista

Obtenido de "http://tesla.us.es/wiki/index.php/Efecto_Doppler"

Herramientas:

Herramientas personales
TOOLBOX
LANGUAGES
licencia de Creative Commons
 Aviso legal - Acerca de Laplace