Incertidumbre en los datos

De Laplace

Revisión de 11:02 18 mar 2010

1 Introducción

En Ingeniería y en las Ciencias Experimentales, a diferencia de en Matemáticas, la mayoría de las cantidades no son conocidas exactamente (salvo que se trate de factores numéricos como 2, 10 o π). Los datos y resultados de cálculos físicos proceden en última instancia de la experiencia y por tanto están sujetos a incertidumbre.

Así, por ejemplo, la aceleración de la gravedad en la superficie terrestre no es exactamente sino una cantidad que varía de punto a punto y cuyo valor conocido está limitado por la precisión de los aparatos experimentales empleados para medirla.

Por esta razón, en Ingeniería o Física no existen las cantidades con infinitos decimales, ya que esto implicaría un conocimiento perfecto de un dato experimental. Esto quiere decir que si medimos, por ejemplo, una resistencia y obtenemos un valor de aproximadamente 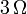, y queremos hallar la conductancia, su valor no puede ser

ya que esto significaría que conocemos todos los decimales de la inversa, aun cuando la cantidad original era solo aproximada. Un valor de

sería probablemente más correcto.

2 Cifras significativas

El primer factor que nos da información sobre la certidumbre de un dato es el número de cifras significativas. Éstas son las que, como su nombre indica, nos dan información detallada sobre el valor de la cantidad.

Como regla básica (que luego matizaremos) podemos definirlo como el número de cifras del dato, sin contar los ceros iniciales o finales. Veamos algunos ejemplos:

2373 Ω

Tiene cuatro cifras significativas.

12.45 V

Tiene también cuatro cifras significativas. La posición del punto decimal es irrelevante. Por ello no hay que confundir el número de cifras significativas con el número de decimales.

0.00987 A

Tiene tres cifras significativas. Los ceros iniciales nos informan del orden de magnitud de la cantidad, pero no de su precisión. Esto se ve más claramente en la notación científica de un número

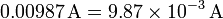
En esta notación, cada cantidad se expresa como el producto de dos: la mantisa, formada por todas las cifras significativas, siendo mayor que 1 y menor que 10, y el exponente, que nos informa del orden de magnitud de la cantidad, que podríamos escribir como 9.87 mA

24.50 Ω

Tiene cuatro cifras significativas. En este caso, el cero final es una cifra significativa, ya que si no sería superfluo. Por ello, no es lo mismo dar un resultado como 24.50 que darlo como 24.5 ya que la primera forma corresponde a una medida más precisa.

45000 m

En este caso tenemos una situación ambigua, ya que el número de cifras significativas podría ser 2, 3, 4 o 5, según que los ceros finales aporten información sobre la mantisa o sólo sobre el orden de magnitud. Esta ambigüedad, de nuevo, desaparece si expresamos el número en notación científica, ya que no es lo mismo 4.5×10⁻⁴m que 4.5000×10⁻⁴m.

El último ejemplo nos muestra que la expresión normal de un número no proporciona suficiente información sobre el número de cifras significativas. Para completar esta información debemos acotar la posible incertidumbre (o error) de una cantidad.