Efecto Doppler
De Laplace
(→=Caso de que los dos estén en movimiento) |
(→Efecto Doppler para ondas sonoras) |
||
| Línea 2: | Línea 2: | ||
==Efecto Doppler para ondas sonoras== | ==Efecto Doppler para ondas sonoras== | ||
===Caso de un observador en movimiento=== | ===Caso de un observador en movimiento=== | ||
| + | Consideremos en primer lugar el caso de una fuente en reposo respecto al medio circundante (el aire). Esta fuente emite ondas de frecuencia <math>f</math>, o equivalentemente, emite crestas de la onda espaciadas un periodo <math>T=1/f</math>. Estas ondas se propagan el el aire radialmente con velocidad <math>c</math>. La distancia entre crestas sucesivas, en el sistema de la fuente, será <math>\lambda = cT</math>. | ||
| + | |||
| + | Queremos determinar la frecuencia que mide un observador que se acerca o se aleja radialmente de la fuente. Al estar la fuente, el observador y la dirección de propagación alineadas, podemos usar cantidades escalares, en lugar de vectoriales, y llamar <math>v_0</math> a la velocidad de este observador. | ||
| + | |||
| + | Tomaremos <math>v_o > 0</math> si el observador se aleja de la fuente y negativa si se acerca a ella. | ||
| + | |||
| + | Cuando el observador se aleja de la fuente, las crestas llegan a él con un intervalo mayor que con el que fueron emitidas, ya que cada cresta debe recorrer una distancia adicional para alcanzar al observador, la que éste ha recorrido en el tiempo intermedio. | ||
| + | |||
| + | Supongamos que una cresta llega al observador en un instante <math>t</math>. La siguiente llegará en un instante <math>t+T'</math>, en este tiempo el observador a recorrido una distancia | ||
| + | |||
| + | <math>x_o = v_oT'\,</math> | ||
| + | |||
| + | En el mismo tiempo, la creta habrá recorrido una distancia igual a la suma de la longitud de onda <math>\lambda=cT</math> y la distancia que se alejado el observador, esto es | ||
| + | |||
| + | <center><math>c T' = c T + v_o T'\,</math></center> | ||
| + | |||
| + | Despejando | ||
| + | |||
| + | <center><math>T' = \frac{cT}{c-v_o}</math></center> | ||
| + | |||
| + | y la frecuencia medida por el observador es | ||
| + | |||
| + | <center><math>f' = \frac{1}{T'}=\left(1-\frac{v_o}{c}\right)f</math></center> | ||
| + | |||
| + | El observador mide una frecuencia menor cuando el observador se aleja, y una mayor cuando se acerca. | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
===Caso de una fuente en movimiento=== | ===Caso de una fuente en movimiento=== | ||
===Caso de que los dos estén en movimiento=== | ===Caso de que los dos estén en movimiento=== | ||
Revisión de 10:36 17 mar 2010
Contenido |
1 Introducción
2 Efecto Doppler para ondas sonoras
2.1 Caso de un observador en movimiento
Consideremos en primer lugar el caso de una fuente en reposo respecto al medio circundante (el aire). Esta fuente emite ondas de frecuencia f, o equivalentemente, emite crestas de la onda espaciadas un periodo T = 1 / f. Estas ondas se propagan el el aire radialmente con velocidad c. La distancia entre crestas sucesivas, en el sistema de la fuente, será λ = cT.
Queremos determinar la frecuencia que mide un observador que se acerca o se aleja radialmente de la fuente. Al estar la fuente, el observador y la dirección de propagación alineadas, podemos usar cantidades escalares, en lugar de vectoriales, y llamar v0 a la velocidad de este observador.
Tomaremos vo > 0 si el observador se aleja de la fuente y negativa si se acerca a ella.
Cuando el observador se aleja de la fuente, las crestas llegan a él con un intervalo mayor que con el que fueron emitidas, ya que cada cresta debe recorrer una distancia adicional para alcanzar al observador, la que éste ha recorrido en el tiempo intermedio.
Supongamos que una cresta llega al observador en un instante t. La siguiente llegará en un instante t + T', en este tiempo el observador a recorrido una distancia
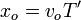
En el mismo tiempo, la creta habrá recorrido una distancia igual a la suma de la longitud de onda λ = cT y la distancia que se alejado el observador, esto es
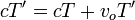
Despejando
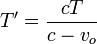
y la frecuencia medida por el observador es
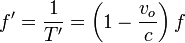
El observador mide una frecuencia menor cuando el observador se aleja, y una mayor cuando se acerca.





