Centro de masas de sistemas continuos

De Laplace

(Diferencias entre revisiones)

Revisión de 18:07 9 mar 2010

Contenido

1 Enunciado
2 Solución
- 2.1 Barra recta
- 2.2 Barra semicircular

1 Enunciado

Calcula por integración la posición del centro de masas de estos dos sistemas

Una barra homogénea delgada de longitud $h$ y masa $M$ .
Una barra homogénea delgada en forma de semicírculo de radio $a$ y masa $M$ .

2 Solución

Para un sistema discreto la posición del centro de masas (CM) viene dada por la expresión

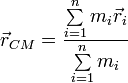
$\displaystyle \vec{r}_{CM} = \frac{\sum\limits_{i=1}^n m_i\vec{r}_i}{\sum\limits_{i=1}^n m_i}$

donde $m i$ es la masa de cada partícula y 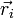$\vec{r}_i$ su vector de posición. Cuando tratamos con un sistema continua, la expresión se transforma según el cambio

$m_i\to\mathrm{d}m \qquad \qquad \qquad \vec{r}_i \to \vec{r}$

Así, en un sistema continuo la posición del centro de masas viene dada por la expresión

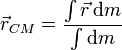
$\displaystyle \vec{r}_{CM} = \frac{\int \vec{r}\,\mathrm{d}m}{\int \mathrm{d}m}$

siendo $\vec{r}$ un vector que recorre cada uno de los puntos del sistema y $d m$ la masa infinitesimal asociada a cada uno de esos puntos.

2.1 Barra recta

Consideramos el caso de una barra homogénea delgada de masa $M$ y longitud $h$ . Lo primero que hay que hacer es escoger un sistema de ejes para describir la posición de cada punto de la barra. Elegimos el eje $O X$ de modo que coincida con la barra y situamos el origen en su extremo izquierdo. Con esta elección la posición de un punto genérico de la barra viene dada por el vector de posición

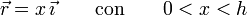
$\vec{r} = x\,\vec{\imath} \qquad \mathrm{con} \qquad 0<x<h$

La variable $x$ es la etiqueta que identifica a cada punto de la barra.

Ahora consideramos que en cada punto de la barra hay un pequeño trocito de barra de longitud $d x$ y masa $d m$ . La d delante de la $x$ y la $m$ sólo significa que la longitud del elemento y su masa son muy pequeñas. ¿Cuanto vale está masa?.

Como la barra es homogénea, podemos definir una densidad lineal de masa como el cociente de su masa por su longitud

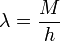
$\lambda = \frac{M}{h}$

Con esto, si el trocito de barra tiene una longitud $d x$ , su masa es

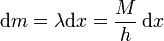
$\mathrm{d}m = \lambda\mathrm{d}x = \frac{M}{h}\,\mathrm{d}x$

Ahora podemos calcular las integrales en la expresión de 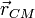$\vec{r}_{CM}$ . La integral en el denominador es la suma de las masas de todos los puntos que podemos considerar en la barra, esto es, su masa completa

$\int\mathrm{d}m = \int\limits_0^h\lambda\,\mathrm{d}x = \lambda\int\limits_0^h\mathrm{d}x = \lambda\,h = M$

La integral en el numerador es

$\int\vec{r}\,\mathrm{d}m = \int\limits_0^h (x\,\vec{\imath})\,\lambda\,\mathrm{d}x = \vec{\imath}\lambda\int\limits_0^h x\,\mathrm{d}x =\vec{\imath}\,\lambda \left[\frac{x^2}{2}\right]_0^h = \frac{1}{2}\lambda\,h^2 = \frac{1}{2}M\,h$

El vector $\vec{\imath}$ y la densidad de masa $λ$ pueden salir de la integral pues no dependen de $x$ , es decir, son iguales no importa en que punto de la barra estemos.

Con esto el vector de posición del CM de la barra respecto de su extremo izquierdo es

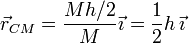
$\vec{r}_{CM} = \frac{Mh/2}{M}\vec{\imath} = \frac{1}{2}h\,\vec{\imath}$

Es decir, para encontrar el CM nos situamos en el extremo izquierdo de la barra y nos desplazamos hacia la derecha una longitud igual a la mitad de su longitud. El CM se sitúa en el centro de la barra. Esto es lógico, pues los ejes de simetría de la barra pasan todos por su centro, por lo que el CM debe situarse en él.

Centro de masas de sistemas continuos

De Laplace

Revisión de 18:07 9 mar 2010

Contenido

1 Enunciado

2 Solución

2.1 Barra recta

2.2 Barra semicircular

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES

@@ Línea 75: / Línea 75: @@
 igual a la mitad de su longitud. El CM se sitúa en el centro de la barra. Esto es lógico, pues los ejes de simetría de la barra
 pasan todos por su centro, por lo que el CM debe situarse en él.
+=== Barra semicircular ===