Energía potencial
De Laplace
(→Energía potencial) |
(→Ejemplos) |
||
| Línea 29: | Línea 29: | ||
==Ejemplos== | ==Ejemplos== | ||
===Peso=== | ===Peso=== | ||
| + | Tomando como origen la superficie terrestre (o, en general, una altura de referencia) la energía potencial debida a una fuerza constante, como el peso la calculamos a partir del trabajo elemental | ||
| + | |||
| + | <center><math>\mathbf{F}=-mg\mathbf{k}</math>{{qquad}}{{qquad}}<math>\mathrm{d}\mathbf{r}=\mathrm{d}x\mathbf{i}+\mathrm{d}y\mathbf{j}+\mathrm{d}z\mathbf{k}</math>{{qquad}}{{qquad}}<math>\mathbf{F}\cdot\mathrm{d}\mathbf{r}=-mg\,\mathrm{d}z</math> | ||
| + | </center> | ||
| + | |||
| + | Integrando esta cantidad | ||
| + | <center><math>U(\mathbf{r}) =-\int_0^z(-mg\,\mathrm{d}z)= mg z\,</math></center> | ||
| + | |||
| + | La energía potencial es proporcional a la altura. Si el punto donde hallamos esta energía está sobre el nivel de referencia, su energía potencial será positiva. Si esta por debajo, su energía potencial será negativa. | ||
| + | |||
===Ley de Hooke=== | ===Ley de Hooke=== | ||
| - | === | + | ====En una dimensión==== |
| - | + | Supongamos un oscilador armónico en el cual una partícula sujeta a un muelle está obligada a moverse a lo largo de una recta. Simedimos la elongación desde la posición de equilibrio, la ley de Hooke queda | |
| - | + | <center><math>\mathbf{F}=-kx\mathbf{i}</math></center> | |
| - | + | y el trabajo elemental | |
| - | + | <center><math>\mathrm{d}\mathbf{r}=\mathrm{d}x\mathbf{i}</math>{{qquad}}{{qquad}}<math>\mathbf{F}\cdot\mathrm{d}\mathbf{r}=-kx\,\mathrm{d}x</math></center> | |
| - | + | Integrando desde la posición de equilibrio, que tomamos como origen de potencial | |
| - | |||
| + | ====En tres dimensiones==== | ||
<center><math>U(\mathbf{r}) = \frac{1}{2}k|\mathbf{r}|^2\,</math></center> | <center><math>U(\mathbf{r}) = \frac{1}{2}k|\mathbf{r}|^2\,</math></center> | ||
| + | ===Fuerza gravitatoria=== | ||
| + | |||
| + | <center><math>U(\mathbf{r}) = -\frac{GMm}{|\mathbf{r}|}\,</math></center> | ||
==Cálculo de la fuerza a partir del potencial== | ==Cálculo de la fuerza a partir del potencial== | ||
Revisión de 00:01 16 feb 2010
Contenido |
1 Fuerzas conservativas
El trabajo realizado por una fuerza cuando una partícula se mueve desde un punto A a un punto B depende en general del camino recorrido. Por ejemplo, una fuerza de rozamiento realiza un trabajo mayor cuanto mayor sea la distancia recorrida, aunque los puntos iniciales y finales sean los mismos en todos los caminos.
Existe una clase de fuerzas, denominadas fuerzas conservativas, para las cuales el trabajo entre dos puntos es independiente del camino que se emplea para ir de uno a otro
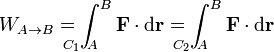
para una fuerza conservativa, por tanto, podemos omitir la indicación de la curva y escribir simplemente
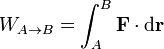
donde la integral se calcula por un camino arbitrario. Eso sí, alguno hay que elegir, sea el que sea.
2 Energía potencial
La independencia del camino permite definir una función denominada energía potencial como el trabajo, cambiado de signo, para ir desde un punto fijo 
(el origen de potencial) hasta el punto que deseemos:
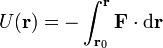
- La independencia del camino es necesaria para que podamos decir que la energía potencial como función solamente del punto
. Si la integral dependiera del camino, para un mismo punto obtendríamos diferentes valores, según por donde hubiéramos llegado a él.
- El origen de potencial es aquel punto para el cual la energía potencial es cero. Dependiendo de cada problema pueden elegirse orígenes de potencial diferentes para la misma fuerza, pero una vez elegido, debe mantenerse siempre el mismo para que los cálculos sean correctos.
- Si dada una fuerza conservativa, calculamos dos energías potenciales diferentes, tomando dos orígenes de potencial distintos, la diferencia entre ellas es una constante (en el sentido de que no resulta una función de la posición )
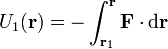
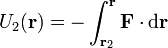
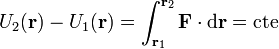
- De su definición como un trabajo resulta que la energía potencial se mide en julios (J) en el SI.
3 Ejemplos
3.1 Peso
Tomando como origen la superficie terrestre (o, en general, una altura de referencia) la energía potencial debida a una fuerza constante, como el peso la calculamos a partir del trabajo elemental
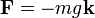
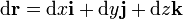
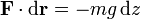
Integrando esta cantidad
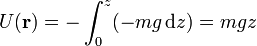
La energía potencial es proporcional a la altura. Si el punto donde hallamos esta energía está sobre el nivel de referencia, su energía potencial será positiva. Si esta por debajo, su energía potencial será negativa.
3.2 Ley de Hooke
3.2.1 En una dimensión
Supongamos un oscilador armónico en el cual una partícula sujeta a un muelle está obligada a moverse a lo largo de una recta. Simedimos la elongación desde la posición de equilibrio, la ley de Hooke queda
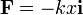
y el trabajo elemental
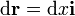
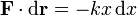
Integrando desde la posición de equilibrio, que tomamos como origen de potencial
3.2.2 En tres dimensiones
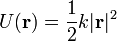
3.3 Fuerza gravitatoria
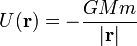
4 Cálculo de la fuerza a partir del potencial
Conocida la energía potencial, puede hallarse la fuerza calculando su gradiente:
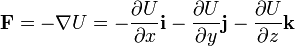
que en el caso de una función dependiente de una sola coordenada se reduce a una derivada ordinaria.
