Fasor
De Laplace
(Diferencias entre revisiones)
(Nueva página: ==Introducción== Existe una forma expresar el movimiento armónico simple. La fórmula de Euler establece una relación entre la exponencial de un número imaginario y las funcio...) |
(→Introducción) |
||
| Línea 1: | Línea 1: | ||
| - | == | + | ==Fórmula de Euler== |
Existe una forma expresar el movimiento armónico simple. La [[fórmula de Euler]] establece una relación entre la exponencial de un número imaginario y las funciones trigonométricas | Existe una forma expresar el movimiento armónico simple. La [[fórmula de Euler]] establece una relación entre la exponencial de un número imaginario y las funciones trigonométricas | ||
| Línea 8: | Línea 8: | ||
<center><math>\cos(x) = \mathrm{Re}\left(\mathrm{e}^{\mathrm{j}x}\right)</math>{{qquad}}{{qquad}}<math>\mathrm{sen}(x) = \mathrm{Im}\left(\mathrm{e}^{\mathrm{j}x}\right)</math></center> | <center><math>\cos(x) = \mathrm{Re}\left(\mathrm{e}^{\mathrm{j}x}\right)</math>{{qquad}}{{qquad}}<math>\mathrm{sen}(x) = \mathrm{Im}\left(\mathrm{e}^{\mathrm{j}x}\right)</math></center> | ||
| + | ==Vectores rotantes== | ||
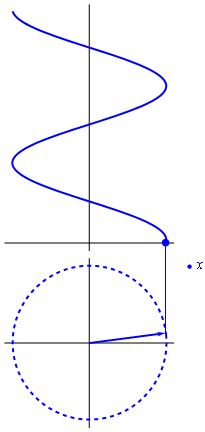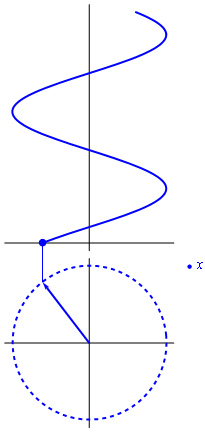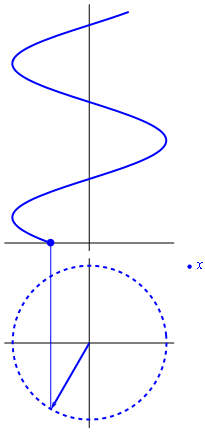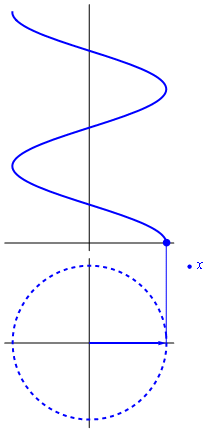
[[Imagen:unfasor.gif|right]]Aplicando esta relación a la solución general del M.A.S. obtenemos | [[Imagen:unfasor.gif|right]]Aplicando esta relación a la solución general del M.A.S. obtenemos | ||
| Línea 18: | Línea 19: | ||
es la llamada ''amplitud compleja'' o ''fasor'' de la variable <math>x</math>. Es un número complejo cuyo módulo es la amplitud del movimiento y cuyo argumento es la constante de fase. | es la llamada ''amplitud compleja'' o ''fasor'' de la variable <math>x</math>. Es un número complejo cuyo módulo es la amplitud del movimiento y cuyo argumento es la constante de fase. | ||
| + | ==Amplitudes complejas== | ||
Aplicando de nuevo la fórmula de Euler obtenemos la parte real y la imaginaria del fasor | Aplicando de nuevo la fórmula de Euler obtenemos la parte real y la imaginaria del fasor | ||
Revisión de 19:30 9 feb 2010
1 Fórmula de Euler
Existe una forma expresar el movimiento armónico simple. La fórmula de Euler establece una relación entre la exponencial de un número imaginario y las funciones trigonométricas
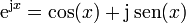
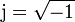
o, equivalentemente,
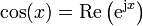
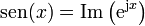
2 Vectores rotantes
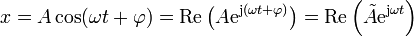
donde
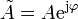
es la llamada amplitud compleja o fasor de la variable x. Es un número complejo cuyo módulo es la amplitud del movimiento y cuyo argumento es la constante de fase.
3 Amplitudes complejas
Aplicando de nuevo la fórmula de Euler obtenemos la parte real y la imaginaria del fasor
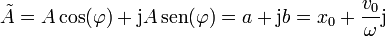
esto es, la amplitud compleja queda completamente determinada por las condiciones iniciales. Vemos que el vector de componentes a y b que definimos anteriormente no es más que la representación del fasor en el plano complejo.
