Ecuaciones de Maxwell

De Laplace

(Diferencias entre revisiones)

Revisión de 11:35 9 feb 2010

1 Introducción

2 Ley de Gauss

Artículo completo: Ley de Gauss

2.1 En forma integral

La ley de Gauss para el campo eléctrico se expresa, en forma integral

$\oint_{\partial\tau} \mathbf{E}\cdot\mathrm{d}\mathbf{S}=\frac{Q_\mathrm{int}}{\varepsilon_0}$

Analizando cada uno de los símbolos que aparecen en esta expresión

2.2 En forma diferencial

2.3 Condición de salto

3 Ley de Faraday

3.1 En forma integral

3.2 En forma diferencial

3.3 Condición de salto

4 Ley de Gauss para el campo magnético

4.1 En forma integral

4.2 En forma diferencial

4.3 Condición de salto

5 Ley de Ampère-Maxwell

5.1 En forma integral

5.2 En forma diferencial

5.3 Condición de salto

6 Tabla de las ecuaciones

Nombre	Ecuación	Condición
Ley de Gauss	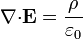$\nabla{\cdot}\mathbf{E} = \frac{\rho}{\varepsilon_0}$	$\mathbf{n}{\cdot}[\mathbf{E}]= \frac{\sigma_s}{\varepsilon_0}$
Ley de Faraday	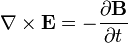$\nabla\times\mathbf{E} = -\frac{\partial \mathbf{B}}{\partial t}$	$\mathbf{n}\times[\mathbf{E}]=\mathbf{0}$
Ley de Gauss para el campo magnético	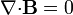$\nabla{\cdot}\mathbf{B} = 0$	$\mathbf{n}{\cdot}[\mathbf{B}]=0\,$
Ley de Ampère-Maxwell	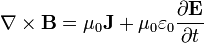$\nabla\times\mathbf{B} = \mu_0\mathbf{J} + \mu_0\varepsilon_0\frac{\partial \mathbf{E}}{\partial t}$	$\mathbf{n}\times[\mathbf{B}] = \mu_0\mathbf{K}$

A su vez, se denominan ecuaciones homogéneas a la ley de Fraday a la de Gauss para el campo magnético, e inhomogéneas (porque aparecen las fuentes) a la de Gauss y la de Ampère-Maxwell.

Por último, dado que estas ecuaciones incluyen derivadas respecto al tiempo, deben ser suplementadas con las condiciones iniciales correspondientes.

7 Condiciones iniciales

8 Ecuaciones de Maxwell en la materia

9 Electro- y magnetostática

@@ Línea 6: / Línea 6: @@
 <center><math>\oint_{\partial\tau} \mathbf{E}\cdot\mathrm{d}\mathbf{S}=\frac{Q_\mathrm{int}}{\varepsilon_0}</math></center>
+Analizando cada uno de los símbolos que aparecen en esta expresión
 ===En forma diferencial===