Ecuaciones de Maxwell

De Laplace

(Diferencias entre revisiones)

Revisión de 10:21 9 feb 2010

Contenido

1 Introducción
2 Ley de Gauss
3 Ley de Faraday
4 Ley de Gauss para el campo magnético
5 Ley de Ampère-Maxwell
6 Tabla de las ecuaciones
7 Ecuaciones de Maxwell en la materia

1 Introducción

2 Ley de Gauss

2.1 En forma integral

2.2 En forma diferencial

2.3 Condición de salto

3 Ley de Faraday

3.1 En forma integral

3.2 En forma diferencial

3.3 Condición de salto

4 Ley de Gauss para el campo magnético

4.1 En forma integral

4.2 En forma diferencial

4.3 Condición de salto

5 Ley de Ampère-Maxwell

5.1 En forma integral

5.2 En forma diferencial

5.3 Condición de salto

6 Tabla de las ecuaciones

Nombre	Ecuación	Condición
Ley de Gauss	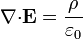$\nabla{\cdot}\mathbf{E} = \frac{\rho}{\varepsilon_0}$	$\mathbf{n}{\cdot}[\mathbf{E}]= \frac{\sigma_s}{\varepsilon_0}$
Ley de Faraday	$\nabla\times\mathbf{E} = -\frac{\partial \mathbf{B}}{\partial t}$	$\mathbf{n}\times[\mathbf{E}]=\mathbf{0}$
Ley de Gauss para el campo magnético	$\nabla{\cdot}\mathbf{B} = 0$	$\mathbf{n}{\cdot}[\mathbf{B}]=0\,$
Ley de Ampère-Maxwell	$\nabla\times\mathbf{B} = \mu_0\mathbf{J} + \mu_0\varepsilon_0\frac{\partial \mathbf{E}}{\partial t}$	$\mathbf{n}\times[\mathbf{B}] = \mu_0\mathbf{K}$

A su vez, se denominan ecuaciones homogéneas a la ley de Fraday a la de Gauss para el campo magnético, e inhomogéneas (porque aparecen las fuentes) a la de Gauss y la de Ampère-Maxwell.

Por último, dado que estas ecuaciones incluyen derivadas respecto al tiempo, deben ser suplementadas con las condiciones iniciales correspondientes.

7 Ecuaciones de Maxwell en la materia

@@ Línea 17: / Línea 17: @@
 ===Condición de salto===
 ==Tabla de las ecuaciones==
+<center>
+{|class="bordeado"
+|-
+! Nombre
+! Ecuación
+! Condición
+|-
+! Ley de Gauss
+| <math>\nabla{\cdot}\mathbf{E}   =  \frac{\rho}{\varepsilon_0}</math>
+| <math>\mathbf{n}{\cdot}[\mathbf{E}]= \frac{\sigma_s}{\varepsilon_0}</math>
+|-
+! Ley de Faraday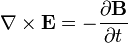
+| <math>\nabla\times\mathbf{E}  =  -\frac{\partial \mathbf{B}}{\partial t}</math>
+| <math>\mathbf{n}\times[\mathbf{E}]=\mathbf{0}</math>
+|-
+! Ley de Gauss para el campo magnético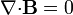
+| <math>\nabla{\cdot}\mathbf{B} =  0</math>
+| <math>\mathbf{n}{\cdot}[\mathbf{B}]=0\,</math>
+|-
+! Ley de Ampère-Maxwell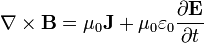
+| <math>\nabla\times\mathbf{B}  =  \mu_0\mathbf{J} + \mu_0\varepsilon_0\frac{\partial \mathbf{E}}{\partial t}</math>
+| <math>\mathbf{n}\times[\mathbf{B}] = \mu_0\mathbf{K}</math>
+|-
+|}
+</center>
+A su vez, se denominan ecuaciones ''homogéneas'' a la ley de Fraday a la de Gauss para el campo magnético, e '''inhomogéneas''' (porque aparecen las fuentes) a la de Gauss y la de Ampère-Maxwell.
+Por último, dado que estas ecuaciones incluyen derivadas respecto al tiempo, deben ser suplementadas con las condiciones iniciales correspondientes.
 ==Ecuaciones de Maxwell en la materia==
 [[Categoría:Ecuaciones de Maxwell]]