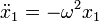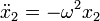Movimiento armónico simple
De Laplace
(Diferencias entre revisiones)
(→Combinación de funciones trigonométricas) |
(→Combinación de funciones trigonométricas) |
||
| Línea 21: | Línea 21: | ||
Para resolver la ecuación de movimiento de un oscilador armónico, empleando técnicas elementales, observamos que trata de hallar una función cuya segunda derivada sea proporcional a la propia función. Es fácil encontrar dos funciones que cumplen esta condición | Para resolver la ecuación de movimiento de un oscilador armónico, empleando técnicas elementales, observamos que trata de hallar una función cuya segunda derivada sea proporcional a la propia función. Es fácil encontrar dos funciones que cumplen esta condición | ||
| - | <center><math>x_1 = \cos(\omega t)\,</math>{{qquad}}{{qquad}} <math>x_2 = \,\mathrm{sen} | + | <center><math>x_1 = \cos(\omega t)\,</math>{{qquad}}{{qquad}} <math>x_2 = \,\mathrm{sen}(\omega t)</math></center> |
Por simple sustitución comprobamos que se cumple | Por simple sustitución comprobamos que se cumple | ||
Revisión de 18:40 7 feb 2010
Contenido |
1 Introducción
El movimiento armónico simple (o, abreviadamente, M.A.S.) es el descrito por una partícula que se mueve a lo largo de una recta verificando la ley de Hooke

Por tratarse de un movimiento rectilíneo, puede reducirse el movimiento a una sola componente
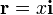
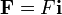
de forma que la ecuación de movimiento se reduce a

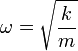
La solución de esta ecuación diferencial, con las condiciones iniciales
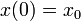
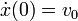
es la forma general de un movimiento armónico simple.
2 Combinación de funciones trigonométricas
Para resolver la ecuación de movimiento de un oscilador armónico, empleando técnicas elementales, observamos que trata de hallar una función cuya segunda derivada sea proporcional a la propia función. Es fácil encontrar dos funciones que cumplen esta condición
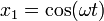
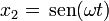
Por simple sustitución comprobamos que se cumple