Campo debido a dos planos paralelos
De Laplace
(Nueva página: ==Enunciado== Un condensador de placas planas puede aproximarse por dos dos planos paralelos, separados una distancia <math>a</math>. Uno de ellos, situado en <math>z=-a/2</math> pose...) |
(→Solución) |
||
| (3 ediciones intermedias no se muestran.) | |||
| Línea 1: | Línea 1: | ||
==Enunciado== | ==Enunciado== | ||
| - | Un condensador de placas planas puede aproximarse por dos dos planos paralelos, separados una distancia <math>a</math>. Uno de ellos, situado en <math>z=-a/2</math> posee una distribución de carga uniforme <math>\sigma_0</math>, mientras que la del otro, situado en <math>z=a/2</math> es <math>-\sigma_0</math>. Halle el campo eléctrico en todos los puntos del espacio. | + | [[Imagen:2planoscargados01.gif|right]]Un condensador de placas planas puede aproximarse por dos dos planos paralelos, separados una distancia <math>a</math>. Uno de ellos, situado en <math>z=-a/2</math> posee una distribución de carga uniforme <math>\sigma_0</math>, mientras que la del otro, situado en <math>z=a/2</math> es <math>-\sigma_0</math>. Halle el campo eléctrico en todos los puntos del espacio. |
==Solución== | ==Solución== | ||
| Línea 25: | Línea 25: | ||
Para superponer estos campos, dividimos el espacio en tres regiones: | Para superponer estos campos, dividimos el espacio en tres regiones: | ||
| + | [[Imagen:2planoscargados02.gif|right]] | ||
;Por debajo del plano inferior (<math>z<-a/2</math>): En esta zona los campos son iguales y opuestos | ;Por debajo del plano inferior (<math>z<-a/2</math>): En esta zona los campos son iguales y opuestos | ||
| Línea 36: | Línea 37: | ||
<center><math>\mathbf{E} = \mathbf{E}_1 + \mathbf{E}_2 = \frac{\sigma_0}{2\varepsilon_0}\mathbf{u}_z-\frac{\sigma_0}{2\varepsilon_0}\mathbf{u}_z = \mathbf{0}</math></center> | <center><math>\mathbf{E} = \mathbf{E}_1 + \mathbf{E}_2 = \frac{\sigma_0}{2\varepsilon_0}\mathbf{u}_z-\frac{\sigma_0}{2\varepsilon_0}\mathbf{u}_z = \mathbf{0}</math></center> | ||
| + | |||
| + | Tenemos entonces que dos planos infinitos cargados uniformemente con cargas iguales y opuestas producen un campo uniforme entre los dos planos y nulo en el espacio exterior a los planos. | ||
| + | |||
| + | Nótese que no es que un plano impida que el campo del otro llegue al otro lado. Cada campo de cada plano se extiende hasta el infinito. Lo que ocurre es que el campo debido a las cargas de un plano anula el campo de las cargas del otro en el espacio exterior a los planos. | ||
| + | |||
| + | El campo total posee una discontinuidad al atravesar cada uno de los planos, como corresponde a la presencia de una densidad de carga superficial. En <math>z = -a/2</math> | ||
| + | |||
| + | <center><math>\mathbf{n}\cdot[\mathbf{E}] = \mathbf{u}_z\cdot\left(\frac{\sigma_0}{\varepsilon_0}\mathbf{u}_z-\mathbf{0}\right) = \frac{\sigma_0}{\varepsilon_0}</math></center> | ||
| + | |||
| + | y en <math>z = a/2</math> | ||
| + | |||
| + | <center><math>\mathbf{n}\cdot[\mathbf{E}] = \mathbf{u}_z\cdot\left(\mathbf{0}-\frac{\sigma_0}{\varepsilon_0}\mathbf{u}_z\right) = -\frac{\sigma_0}{\varepsilon_0}</math></center> | ||
| + | |||
[[Categoría:Problemas de electrostática en el vacío]] | [[Categoría:Problemas de electrostática en el vacío]] | ||
última version al 20:49 8 ene 2010
1 Enunciado
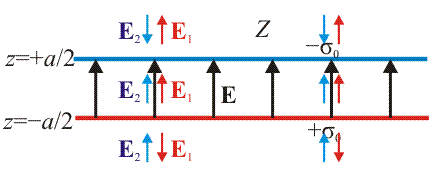
Un condensador de placas planas puede aproximarse por dos dos planos paralelos, separados una distancia a. Uno de ellos, situado en z = − a / 2 posee una distribución de carga uniforme σ0, mientras que la del otro, situado en z = a / 2 es − σ0. Halle el campo eléctrico en todos los puntos del espacio.2 Solución
Este problema puede resolverse por simple superposición de los campos de los planos individuales.
El campo debido a un plano cargado uniformenente situado en z = 0 es
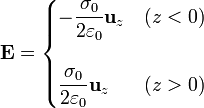
Si este plano está en z = − a / 2 simplemente trasladamos la coordenada y ya tenemos el campo del primer plano
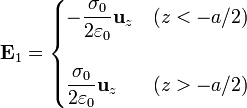
Para el segundo plano, cambiamos a por − a y σ0 por − σ0, lo que nos deja
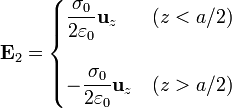
Para superponer estos campos, dividimos el espacio en tres regiones:
- Por debajo del plano inferior (z < − a / 2)
- En esta zona los campos son iguales y opuestos
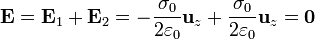
- Por debajo del plano inferior ( − a / 2 < z < a / 2)
- En esta zona los campos son iguales y en el mismo sentido
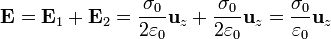
- Por encima del plano superior (z > a / 2)
- En esta zona, de nuevo, los campos son iguales y opuestos
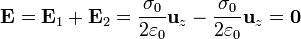
Tenemos entonces que dos planos infinitos cargados uniformemente con cargas iguales y opuestas producen un campo uniforme entre los dos planos y nulo en el espacio exterior a los planos.
Nótese que no es que un plano impida que el campo del otro llegue al otro lado. Cada campo de cada plano se extiende hasta el infinito. Lo que ocurre es que el campo debido a las cargas de un plano anula el campo de las cargas del otro en el espacio exterior a los planos.
El campo total posee una discontinuidad al atravesar cada uno de los planos, como corresponde a la presencia de una densidad de carga superficial. En z = − a / 2
![\mathbf{n}\cdot[\mathbf{E}] = \mathbf{u}_z\cdot\left(\frac{\sigma_0}{\varepsilon_0}\mathbf{u}_z-\mathbf{0}\right) = \frac{\sigma_0}{\varepsilon_0}](/wiki/images/math/7/7/1/7718e1440e6af69d71756da4007d2235.png)
y en z = a / 2
![\mathbf{n}\cdot[\mathbf{E}] = \mathbf{u}_z\cdot\left(\mathbf{0}-\frac{\sigma_0}{\varepsilon_0}\mathbf{u}_z\right) = -\frac{\sigma_0}{\varepsilon_0}](/wiki/images/math/6/4/8/64819bf9d32926643d6684d6375ad542.png)