Una varilla y una carga
De Laplace
(→Trabajo para mover la carga entre <math>A</math> y <math>B</math>) |
(→Flujo del campo eléctrico a través de la superficie esférica=) |
||
| (15 ediciones intermedias no se muestran.) | |||
| Línea 7: | Línea 7: | ||
# ¿Qué trabajo habría que realizar para mover la carga puntual entre los puntos <math>A</math> al <math>B</math>? (ver figura) | # ¿Qué trabajo habría que realizar para mover la carga puntual entre los puntos <math>A</math> al <math>B</math>? (ver figura) | ||
| - | + | ==Flujo del campo eléctrico a través de la superficie esférica== | |
| - | + | ||
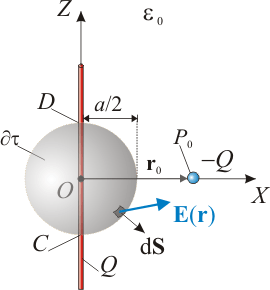
Tal como se indica en las figuras, adoptaremos un sistema de referencia cartesiano con origen en el centro de la varilla cargada, la cuál va a ser colineal con el eje <math>\ OZ</math>. Además, consideraremos que la carga puntual <math>\ -Q</math> se halla en el eje <math>\ OX</math>. | Tal como se indica en las figuras, adoptaremos un sistema de referencia cartesiano con origen en el centro de la varilla cargada, la cuál va a ser colineal con el eje <math>\ OZ</math>. Además, consideraremos que la carga puntual <math>\ -Q</math> se halla en el eje <math>\ OX</math>. | ||
| Línea 19: | Línea 18: | ||
<center><math>\lambda_e(\mathbf{r'})=\frac{\mathrm{d}q}{\mathrm{d}l'}=\frac{\Delta q}{\Delta z'}=\frac{Q}{2a}</math></center> | <center><math>\lambda_e(\mathbf{r'})=\frac{\mathrm{d}q}{\mathrm{d}l'}=\frac{\Delta q}{\Delta z'}=\frac{Q}{2a}</math></center> | ||
| - | |||
La expresión del campo eléctrico de una carga puntual es bien conocida, y el cálculo del campo eléctrico creado por un segmento con densidad lineal de carga constante puede verse en el ejercicio [[Campo eléctrico de un segmento cargado]]. | La expresión del campo eléctrico de una carga puntual es bien conocida, y el cálculo del campo eléctrico creado por un segmento con densidad lineal de carga constante puede verse en el ejercicio [[Campo eléctrico de un segmento cargado]]. | ||
| Línea 27: | Línea 25: | ||
<center><math>\left.\begin{array}{r}\displaystyle \oint_{\partial \tau}\!\mathbf{E}\cdot \mathrm{d}\mathbf{S}=\frac{1}{\varepsilon_0} \, q\big|_\tau \\ \\ \displaystyle q\big|_\tau=\int_C^D\!\!\lambda_e(\mathbf{r'})\mathrm{d}l'=\frac{Q}{2a}\int_{-a/2}^{a/2}\!\mathrm{d}z'=\frac{Q}{2}\end{array}\right\}</math> {{tose}} <math style="border:solid green 2px;padding:10px">\oint_{\partial \tau}\!\mathbf{E}\cdot \mathrm{d}\mathbf{S}=\frac{Q}{2\varepsilon_0}</math></center> | <center><math>\left.\begin{array}{r}\displaystyle \oint_{\partial \tau}\!\mathbf{E}\cdot \mathrm{d}\mathbf{S}=\frac{1}{\varepsilon_0} \, q\big|_\tau \\ \\ \displaystyle q\big|_\tau=\int_C^D\!\!\lambda_e(\mathbf{r'})\mathrm{d}l'=\frac{Q}{2a}\int_{-a/2}^{a/2}\!\mathrm{d}z'=\frac{Q}{2}\end{array}\right\}</math> {{tose}} <math style="border:solid green 2px;padding:10px">\oint_{\partial \tau}\!\mathbf{E}\cdot \mathrm{d}\mathbf{S}=\frac{Q}{2\varepsilon_0}</math></center> | ||
| - | + | ==Fuerza sobre la carga puntual== | |
La fuerza sobre la carga puntual <math>\ -Q</math> colocada en el punto <math>\ P_0</math> es igual al resultado de multiplicar dicha carga por el campo eléctrico creado en dicho punto por la distribución de carga de la varilla: | La fuerza sobre la carga puntual <math>\ -Q</math> colocada en el punto <math>\ P_0</math> es igual al resultado de multiplicar dicha carga por el campo eléctrico creado en dicho punto por la distribución de carga de la varilla: | ||
| Línea 52: | Línea 50: | ||
-\frac{\sqrt{2}\ Q^2}{8\pi\varepsilon_0a^2}\ \mathbf{u}_x</math></center> | -\frac{\sqrt{2}\ Q^2}{8\pi\varepsilon_0a^2}\ \mathbf{u}_x</math></center> | ||
| - | + | ==Desarrollo multipolar== | |
El momento monopolar del sistema (que llamaremos <math>\ Q_O</math>) es igual a la suma de todas las cargas puntuales, más la carga total contenida en las distribuciones líneales, superficiales y volumétricas de carga eléctrica que lo constituyen; es decir, es la carga eléctrica total del sistema. En el caso que nos ocupa se tendrá: | El momento monopolar del sistema (que llamaremos <math>\ Q_O</math>) es igual a la suma de todas las cargas puntuales, más la carga total contenida en las distribuciones líneales, superficiales y volumétricas de carga eléctrica que lo constituyen; es decir, es la carga eléctrica total del sistema. En el caso que nos ocupa se tendrá: | ||
| Línea 73: | Línea 71: | ||
<center> {{tose}} <math style="border:solid blue 2px;padding:10px">\mathbf{E}(P)=\mathbf{E}(x,y,z)\approx\frac{1}{4\pi\varepsilon_0}\ \frac{\big(3\mathbf{p}_O\cdot\mathbf{r}\big)\mathbf{r}-|\mathbf{r}|^2\mathbf{p}_O}{|\mathbf{r}|^5}= -\frac{Q\ a}{4\pi\varepsilon_0}\ \frac{\big(2x^2-y^2-z^2\big)\mathbf{u}_x+3xy\mathbf{u}_y+3xz\mathbf{u}_z}{\big(x^2+y^2+z^2\big)^{5/2}}</math></center> | <center> {{tose}} <math style="border:solid blue 2px;padding:10px">\mathbf{E}(P)=\mathbf{E}(x,y,z)\approx\frac{1}{4\pi\varepsilon_0}\ \frac{\big(3\mathbf{p}_O\cdot\mathbf{r}\big)\mathbf{r}-|\mathbf{r}|^2\mathbf{p}_O}{|\mathbf{r}|^5}= -\frac{Q\ a}{4\pi\varepsilon_0}\ \frac{\big(2x^2-y^2-z^2\big)\mathbf{u}_x+3xy\mathbf{u}_y+3xz\mathbf{u}_z}{\big(x^2+y^2+z^2\big)^{5/2}}</math></center> | ||
| - | + | ==Trabajo para mover la carga entre <math>A</math> y <math>B</math>== | |
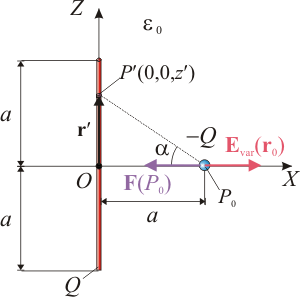
Supongamos una fuerza exterior <math>\mathbf{F}_\mathrm{ext}</math> que actúa sobre a carga <math>\ -Q</math>, haciendo que ésta se mueva de manera cuasi-estacionaria, es decir, pasando por sucesivos estados de equilibrio y constituyendo un proceso reversible (ideal). Para ello debe verificarse que la fuerza neta que actúa sobre la carga (la exterior más la que ejerce el campo eléctrico creado por la varilla) debe ser nula. En consecuencia, el trabajo infinitesimal realizado por dicha fuerza cuando provoca un desplazamiento diferencial de la partícula, <math>\mathrm{d}\mathbf{r}</math>, es: | Supongamos una fuerza exterior <math>\mathbf{F}_\mathrm{ext}</math> que actúa sobre a carga <math>\ -Q</math>, haciendo que ésta se mueva de manera cuasi-estacionaria, es decir, pasando por sucesivos estados de equilibrio y constituyendo un proceso reversible (ideal). Para ello debe verificarse que la fuerza neta que actúa sobre la carga (la exterior más la que ejerce el campo eléctrico creado por la varilla) debe ser nula. En consecuencia, el trabajo infinitesimal realizado por dicha fuerza cuando provoca un desplazamiento diferencial de la partícula, <math>\mathrm{d}\mathbf{r}</math>, es: | ||
| - | <center><math>\mathbf{F}_\mathrm{ext}-Q \mathbf{E}_\mathrm{var}(\mathbf{r})=\mathbf{0}</math> {{tose}} <math>\delta W_\mathrm{ext}=\mathbf{F}_\mathrm{ext}\cdot\mathrm{d}\mathbf{r}=Q | + | [[Imagen:P2_v.gif|left]]<center><math>\mathbf{F}_\mathrm{ext}+\mathbf{F}_\mathrm{var}=\mathbf{F}_\mathrm{ext}-Q \mathbf{E}_\mathrm{var}(\mathbf{r})=\mathbf{0}</math> {{tose}} <math>\delta W_\mathrm{ext}=\mathbf{F}_\mathrm{ext}\cdot\mathrm{d}\mathbf{r}=Q \mathbf{E}_\mathrm{var}(\mathbf{r})\cdot\mathrm{d}\mathbf{r}</math></center> |
El trabajo total realizado en el proceso de llevar la carga puntual negativa desde <math>A</math> hasta <math>B</math>, será proporcional a la circulación entre dichos puntos del campo eléctrico creado por la varilla. Y puesto que éste es un campo electrostático y derivará de un potencial electrostático <math>\phi_\mathrm{var}(\mathbf{r})</math>, dicha circulación será independiente del camino e igual a la diferencia de potencial entre los puntos inicial y final: | El trabajo total realizado en el proceso de llevar la carga puntual negativa desde <math>A</math> hasta <math>B</math>, será proporcional a la circulación entre dichos puntos del campo eléctrico creado por la varilla. Y puesto que éste es un campo electrostático y derivará de un potencial electrostático <math>\phi_\mathrm{var}(\mathbf{r})</math>, dicha circulación será independiente del camino e igual a la diferencia de potencial entre los puntos inicial y final: | ||
| Línea 89: | Línea 87: | ||
Si esta variación es positiva, la fuerza externa habrá realizado trabajo; si es negativa, es el campo electrostático de la varilla el que ha realizado el trabajo y la fuerza exterior sólo ha intervenido para que el proceso sea cuasi-estacionario. | Si esta variación es positiva, la fuerza externa habrá realizado trabajo; si es negativa, es el campo electrostático de la varilla el que ha realizado el trabajo y la fuerza exterior sólo ha intervenido para que el proceso sea cuasi-estacionario. | ||
| - | Por tanto, para responder | + | Por tanto, para responder a este apartado sólo hay que calcular la diferencia de potencial entre los puntos inicial y final, pero para ello, no va ser necesario calcular el valor del potencial creado por la varilla en cada punto del espacio. Nótese que el punto <math>\ B</math> y el punto <math>\ A</math> se encuentran a igual distancia de sendos puntos simétricos de la varilla, <math>\ P'(0,0,z')</math> y <math>\ P'(0,0,-z')</math>, en cada uno de los cuales hay la misma cantidad infinitesimal de carga <math>\ \mathrm{d}q'=(Q/2a)\mathrm{d}z'</math>. Como el potencial electrostático es una magnitud escalar cuyo valor en un punto sólo depende de la distancia a cada carga fuente y del valor de ésta, la conclusión es que... |
| + | |||
| + | <center><math style="border:solid magenta 2px;padding:10px">\ \phi_\mathrm{var}(B)=\phi_\mathrm{var}(A)</math> {{tose}} <math style="border:solid cyan 2px;padding:10px">\Delta W_\mathrm{ext}^{A\rightarrow B}=\Delta U_e^{A\rightarrow B}=-Q\big[\phi_\mathrm{var}(B)-\phi_\mathrm{var}(A)\big]=0</math></center> | ||
| + | |||
| + | Es decir, no se realiza trabajo neto ya que el potencial electrostático creado por la varilla y, por tanto, la energía potencial de la carga puntual en los puntos <math>\ A</math> y <math>\ B</math> es idéntica. | ||
| + | Veamos analíticamente la igualdad del valor del potencial en dichos puntos, dados por los vectores posición <math>\ \mathbf{r}_A=a(\mathbf{u}_x-\mathbf{u}_z)</math> y <math>\ \mathbf{r}_B=a(\mathbf{u}_x+\mathbf{u}_z)</math>. Aplicando la expresión general del potencial para distribuciones lineales de carga, se tendrá: | ||
| + | <center><math>\ \phi_\mathrm{var}(\mathbf{r})=\frac{1}{4\pi\varepsilon_0}\int_\mathrm{var}\!\frac{\lambda_e(\mathbf{r'})}{|\mathbf{r}-\mathbf{r'}|}\ \mathrm{d}l'</math> {{tose}} <math>\left\{\begin{array}{l} \displaystyle \phi_\mathrm{var}(\mathbf{r}_A)=\frac{Q}{8\pi\varepsilon_0a}\int_{-a}^a\!\frac{\mathrm{d}z'}{\sqrt{a^2+(a+z')^2}}=\phi_\mathrm{var}(A)\\ \\ \displaystyle \phi_\mathrm{var}(\mathbf{r}_B)=\frac{Q}{8\pi\varepsilon_0a}\int_{-a}^a\!\frac{\mathrm{d}z'}{\sqrt{a^2+(a-z')^2}}=\phi_\mathrm{var}(B)\end{array}\right.</math></center> | ||
| + | Y con estas dos integrales definidas se obtiene el mismo resultado, pues realizando el cambio de variable <math>\ u=-z'</math> en cualquiera de ellas, ambas integrales pasan a ser idénticas, con lo que se demuestra la igualdad <math>\ \phi_\mathrm{var}(B)=\phi_\mathrm{var}(A)</math> | ||
[[Categoría:Problemas de electrostática en el vacío]] | [[Categoría:Problemas de electrostática en el vacío]] | ||
última version al 11:22 17 ene 2010
Contenido |
1 Enunciado
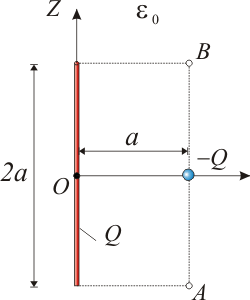
Una carga eléctrica Q está uniformemente distribuida a lo largo de un segmento rectilíneo de longitud 2a. A una distancia a del punto medio de dicho segmento y en dirección perpendicular a éste, se halla una carga puntual − Q.- Calcule el flujo del campo eléctrico a través de una superficie esférica de radio a / 2 centrada en el punto medio del segmento cargado (punto O).
- Obtenga la fuerza que actúa sobre la carga puntual.
- Calcule los momentos monopolar y dipolar de la distribución de carga descrita. Proponga expresiones aproximadas para el potencial y el campo eléctrico en puntos suficientemente alejados de la distribución.
- ¿Qué trabajo habría que realizar para mover la carga puntual entre los puntos A al B? (ver figura)
2 Flujo del campo eléctrico a través de la superficie esférica
Tal como se indica en las figuras, adoptaremos un sistema de referencia cartesiano con origen en el centro de la varilla cargada, la cuál va a ser colineal con el eje 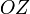 . Además, consideraremos que la carga puntual
. Además, consideraremos que la carga puntual 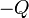 se halla en el eje
se halla en el eje 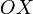 .
.
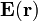 , a través de una superficie esférica
, a través de una superficie esférica 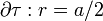 :
:

Nótese que dicho campo debe ser el creado por toda la distribución de carga descrita; es decir, la carga puntual 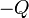 colocada en el punto P0, dado por el vector
colocada en el punto P0, dado por el vector 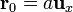 , y la varilla de longitud
, y la varilla de longitud 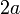 cargada uniformemente con una cantidad
cargada uniformemente con una cantidad  de carga eléctrica, o lo que es lo mismo, con una densidad lineal constante:
de carga eléctrica, o lo que es lo mismo, con una densidad lineal constante:
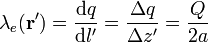
La expresión del campo eléctrico de una carga puntual es bien conocida, y el cálculo del campo eléctrico creado por un segmento con densidad lineal de carga constante puede verse en el ejercicio Campo eléctrico de un segmento cargado.
Sin embargo no es necesario realizar el cálculo explícito de la anterior integral ya que, en virtud de la Ley de Gauss se tiene que dicho flujo del campo eléctrico a través de una superficie cerrada es proporcional a la cantidiad de carga eléctrica encerrada en su interior. Dada las dimensiones y la posición de  respecto del sistema de cargas, se tiene que sólo la mitad de la varilla se halla en el interior de dicha superficie esférica. Como la distribución de carga en la varilla es uniforme, habrá una cantidad de carga
respecto del sistema de cargas, se tiene que sólo la mitad de la varilla se halla en el interior de dicha superficie esférica. Como la distribución de carga en la varilla es uniforme, habrá una cantidad de carga 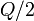 dentro de
dentro de  :
:
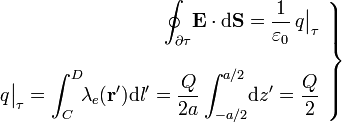

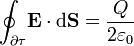
3 Fuerza sobre la carga puntual
La fuerza sobre la carga puntual 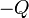 colocada en el punto
colocada en el punto 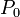 es igual al resultado de multiplicar dicha carga por el campo eléctrico creado en dicho punto por la distribución de carga de la varilla:
es igual al resultado de multiplicar dicha carga por el campo eléctrico creado en dicho punto por la distribución de carga de la varilla:
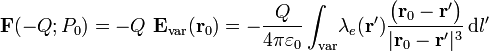
donde 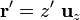 es el vector posición correspondiente a un punto arbitrario de la varilla, P'. Se tendrá entonces...
es el vector posición correspondiente a un punto arbitrario de la varilla, P'. Se tendrá entonces...
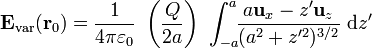
Como ya se ha visto en otros ejercicios relativos a segmentos cargados, para realizar estas dos integrales resulta muy útil el siguiente cambio de variable:


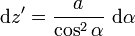
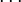 , que llevado a la anterior expresión proporciona el valor de las componentes
, que llevado a la anterior expresión proporciona el valor de las componentes 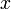 y
y 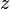 del campo eléctrico creado por la varilla en
del campo eléctrico creado por la varilla en 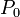 :
:

Es decir, puesto que la carga puntual se halla en un eje de simetría de la distribución lineal, la fuerza que actúa sobre aquélla sólo tiene componente en la dirección 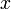 :
:
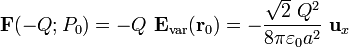
4 Desarrollo multipolar
El momento monopolar del sistema (que llamaremos 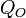 ) es igual a la suma de todas las cargas puntuales, más la carga total contenida en las distribuciones líneales, superficiales y volumétricas de carga eléctrica que lo constituyen; es decir, es la carga eléctrica total del sistema. En el caso que nos ocupa se tendrá:
) es igual a la suma de todas las cargas puntuales, más la carga total contenida en las distribuciones líneales, superficiales y volumétricas de carga eléctrica que lo constituyen; es decir, es la carga eléctrica total del sistema. En el caso que nos ocupa se tendrá:
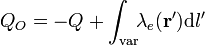


Por su parte, el momento dipolar del sistema calculado respecto del origen del sistema de referencia, 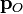 , es...
, es...


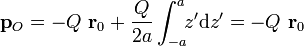
Obsérvese que, como el momento monopolar es nulo, el dipolar no va a depender del punto que se elija como “centro de la distribución”:
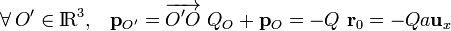
Esto tiene como consecuencia que en puntos del espacio suficientemente alejados de la distribución de carga, el potencial y el campo eléctrico generado por aquélla son, en primera aproximación, los del dipolo 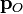 colocado en cualquier punto próximo a dicho distribución. Por tanto, si
colocado en cualquier punto próximo a dicho distribución. Por tanto, si  es un punto que verifica dicha condición, se tendrá...
es un punto que verifica dicha condición, se tendrá...
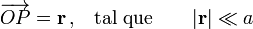

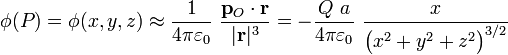


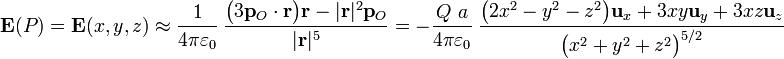
5 Trabajo para mover la carga entre A y B
Supongamos una fuerza exterior 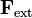 que actúa sobre a carga
que actúa sobre a carga 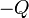 , haciendo que ésta se mueva de manera cuasi-estacionaria, es decir, pasando por sucesivos estados de equilibrio y constituyendo un proceso reversible (ideal). Para ello debe verificarse que la fuerza neta que actúa sobre la carga (la exterior más la que ejerce el campo eléctrico creado por la varilla) debe ser nula. En consecuencia, el trabajo infinitesimal realizado por dicha fuerza cuando provoca un desplazamiento diferencial de la partícula,
, haciendo que ésta se mueva de manera cuasi-estacionaria, es decir, pasando por sucesivos estados de equilibrio y constituyendo un proceso reversible (ideal). Para ello debe verificarse que la fuerza neta que actúa sobre la carga (la exterior más la que ejerce el campo eléctrico creado por la varilla) debe ser nula. En consecuencia, el trabajo infinitesimal realizado por dicha fuerza cuando provoca un desplazamiento diferencial de la partícula, 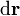 , es:
, es:
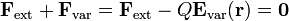

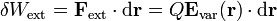
El trabajo total realizado en el proceso de llevar la carga puntual negativa desde A hasta B, será proporcional a la circulación entre dichos puntos del campo eléctrico creado por la varilla. Y puesto que éste es un campo electrostático y derivará de un potencial electrostático 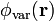 , dicha circulación será independiente del camino e igual a la diferencia de potencial entre los puntos inicial y final:
, dicha circulación será independiente del camino e igual a la diferencia de potencial entre los puntos inicial y final:
![\ \Delta W_\mathrm{ext}^{A\rightarrow B}=Q \int_A^B\! \mathbf{E}_\mathrm{var}\cdot\mathrm{d}\mathbf{r}=-Q\int_A^B\! \mathrm{d}\phi_\mathrm{var}=-Q\big[\phi_\mathrm{var}(B)-\phi_\mathrm{var}(A)\big]](/wiki/images/math/7/e/a/7ead47206baef5b0d20e735a115a6c87.png)
Obsérvese que definiendo la energía potencial electrostática  de la carga puntual negativa en el seno del campo creado por la varilla cargada, como el producto de aquélla por el valor del potencial
de la carga puntual negativa en el seno del campo creado por la varilla cargada, como el producto de aquélla por el valor del potencial 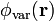 , se llega al resultado ya conocido de que el trabajo realizado por la fuerza externa al cambiar la posición de la carga, es igual a la variación experimentada por dicha energía potencial:
, se llega al resultado ya conocido de que el trabajo realizado por la fuerza externa al cambiar la posición de la carga, es igual a la variación experimentada por dicha energía potencial:
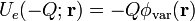


Si esta variación es positiva, la fuerza externa habrá realizado trabajo; si es negativa, es el campo electrostático de la varilla el que ha realizado el trabajo y la fuerza exterior sólo ha intervenido para que el proceso sea cuasi-estacionario.
Por tanto, para responder a este apartado sólo hay que calcular la diferencia de potencial entre los puntos inicial y final, pero para ello, no va ser necesario calcular el valor del potencial creado por la varilla en cada punto del espacio. Nótese que el punto  y el punto
y el punto  se encuentran a igual distancia de sendos puntos simétricos de la varilla,
se encuentran a igual distancia de sendos puntos simétricos de la varilla, 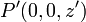 y
y 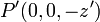 , en cada uno de los cuales hay la misma cantidad infinitesimal de carga
, en cada uno de los cuales hay la misma cantidad infinitesimal de carga 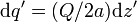 . Como el potencial electrostático es una magnitud escalar cuyo valor en un punto sólo depende de la distancia a cada carga fuente y del valor de ésta, la conclusión es que...
. Como el potencial electrostático es una magnitud escalar cuyo valor en un punto sólo depende de la distancia a cada carga fuente y del valor de ésta, la conclusión es que...


![\Delta W_\mathrm{ext}^{A\rightarrow B}=\Delta U_e^{A\rightarrow B}=-Q\big[\phi_\mathrm{var}(B)-\phi_\mathrm{var}(A)\big]=0](/wiki/images/math/a/f/d/afd3f7d6dc09b0ff4106c1b405ea8067.png)
Es decir, no se realiza trabajo neto ya que el potencial electrostático creado por la varilla y, por tanto, la energía potencial de la carga puntual en los puntos  y
y  es idéntica.
es idéntica.
Veamos analíticamente la igualdad del valor del potencial en dichos puntos, dados por los vectores posición 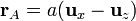 y
y 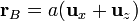 . Aplicando la expresión general del potencial para distribuciones lineales de carga, se tendrá:
. Aplicando la expresión general del potencial para distribuciones lineales de carga, se tendrá:


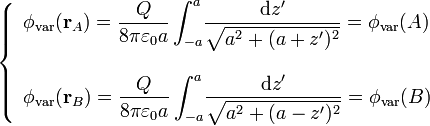
Y con estas dos integrales definidas se obtiene el mismo resultado, pues realizando el cambio de variable 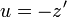 en cualquiera de ellas, ambas integrales pasan a ser idénticas, con lo que se demuestra la igualdad
en cualquiera de ellas, ambas integrales pasan a ser idénticas, con lo que se demuestra la igualdad