Representación de campos vectoriales
De Laplace
(→Campos bidimensionales) |
(→Enlaces) |
||
| (4 ediciones intermedias no se muestran.) | |||
| Línea 13: | Línea 13: | ||
==Campos tridimensionales== | ==Campos tridimensionales== | ||
| + | |||
| + | Este tipo de representaciones se hace prácticamente imposible al pasar al caso general de campos vectoriales en un espacio tridimensional. A las dificultades de la representación espacial de campos escalares en tres dimensiones, se añade el carácter vectorial, que quiere decir que en cada punto los campos vienen descritos por tres cantidades, no por una sola. | ||
| + | |||
| + | Esto hace imposible, por ejemplo, la existencia de "superficies equivectoriales" ya que aunque uniéramos todos los puntos en que una componente tiene el mismo valor, no hay ninguna garantía de que las otras dos componentes tengan el mismo valor en todos los puntos de la misma superficie. | ||
| + | |||
| + | Pueden hacerse representaciones de arrays tridimensionales de vectores, pero incluso ésas son difíciles de visualizar. La forma más eficaz de representar los campos vectoriales es con ayuda de las [[líneas de campo]], concepto que por su importancia, merece un artículo en exclusiva. | ||
| + | |||
| + | |||
| + | <center>[[Imagen:vectores3d.png]] [[Imagen:lineas3d.png]]</center> | ||
==Enlaces== | ==Enlaces== | ||
* '''Siguiente:''' [[Líneas de campo]] | * '''Siguiente:''' [[Líneas de campo]] | ||
* '''Anterior:''' | * '''Anterior:''' | ||
| + | |||
| + | [[Categoría:Campos escalares y vectoriales|50]] | ||
última version al 17:15 2 dic 2007
1 Campos bidimensionales
Un campo vectorial bidimensional es uno que depende solo de dos coordenadas y además posee sólo dos componentes
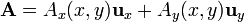
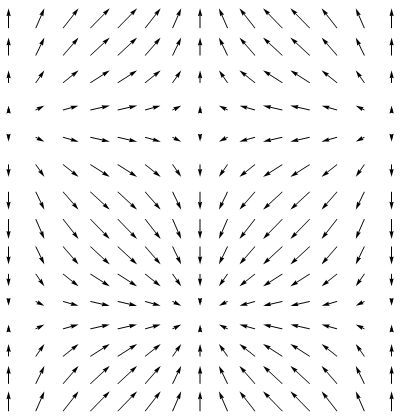
Para este tipo de campos es posible hacer representaciones más o menos ilustrativas, a partir de un array de flechas, que representan el valor del vector en una malla rectangular de puntos.
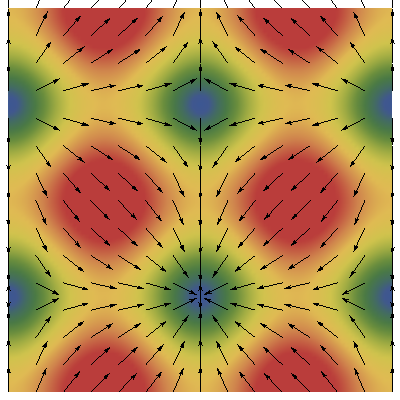
Cuando el módulo varía mucho de un punto a otro, puede ser más ilustrativo combinar la representación de un campo escalar (el módulo del campo vectorial) con un array de vectores unitarios que indican la dirección.
2 Campos tridimensionales
Este tipo de representaciones se hace prácticamente imposible al pasar al caso general de campos vectoriales en un espacio tridimensional. A las dificultades de la representación espacial de campos escalares en tres dimensiones, se añade el carácter vectorial, que quiere decir que en cada punto los campos vienen descritos por tres cantidades, no por una sola.
Esto hace imposible, por ejemplo, la existencia de "superficies equivectoriales" ya que aunque uniéramos todos los puntos en que una componente tiene el mismo valor, no hay ninguna garantía de que las otras dos componentes tengan el mismo valor en todos los puntos de la misma superficie.
Pueden hacerse representaciones de arrays tridimensionales de vectores, pero incluso ésas son difíciles de visualizar. La forma más eficaz de representar los campos vectoriales es con ayuda de las líneas de campo, concepto que por su importancia, merece un artículo en exclusiva.


3 Enlaces
- Siguiente: Líneas de campo
- Anterior:





