Visualización de campos escalares en dos dimensiones
De Laplace
(→Gráficas mixtas) |
(→Enlaces) |
||
| (Una edición intermedia no se muestra.) | |||
| Línea 25: | Línea 25: | ||
* o diagramas 3D coloreados según la altura. | * o diagramas 3D coloreados según la altura. | ||
* o diagramas 3D con curvas de nivel | * o diagramas 3D con curvas de nivel | ||
| - | * o | + | * o todo junto |
<center>[[Imagen:contourcolor.png|300px]] [[Imagen:elevacioncolor.png|300px]]</center> | <center>[[Imagen:contourcolor.png|300px]] [[Imagen:elevacioncolor.png|300px]]</center> | ||
| - | |||
<center>[[Imagen:elevacionnivel.png|300px]] [[Imagen:elevacionnivelcolor.png|300px]]</center> | <center>[[Imagen:elevacionnivel.png|300px]] [[Imagen:elevacionnivelcolor.png|300px]]</center> | ||
| Línea 41: | Línea 40: | ||
* '''Anterior:''' [[Concepto de campo]] | * '''Anterior:''' [[Concepto de campo]] | ||
| - | [[Categoría: | + | [[Categoría:Campos escalares y vectoriales|20]] |
última version al 18:13 2 dic 2007
Contenido |
1 Introducción
El concepto de campo en general, y de campo escalar en particular, es abstracto (hemos de imaginar que llenando el espacio hay algo que varía de un punto a otro) por lo que se hace necesario inventar formas de representar los campos escalares.
Cuando tenemos un campo dependiente de solo dos variables, 
e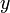 
, existen varias posibilidades:
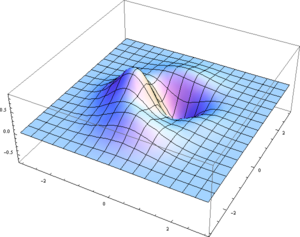
2 Elevación
Una es una representación 3D, como la altura de una montaña
3 Mapa de densidades
Otra es emplear un mapa de densidades, que asigna distintos colores según el valor de la función.
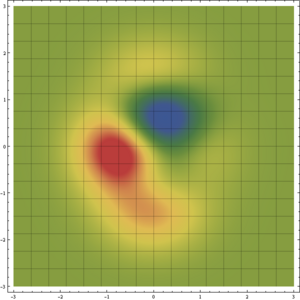
4 Curvas de nivel
Otra posibilidad es emplear curvas de nivel, que unen los puntos en los que la función tiene el mismo valor.
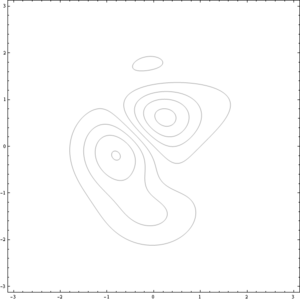
5 Gráficas mixtas
Evidentemente, estas posibilidades se pueden combinar y
- usar curvas de nivel junto con colores, como en los mapas topográficos,
- o diagramas 3D coloreados según la altura.
- o diagramas 3D con curvas de nivel
- o todo junto
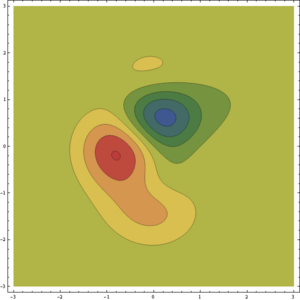
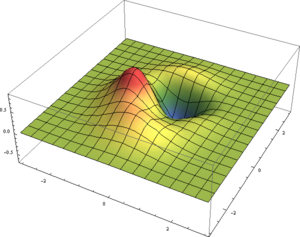
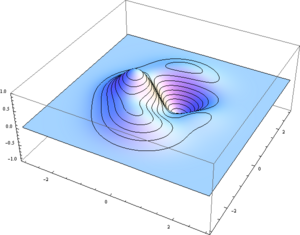
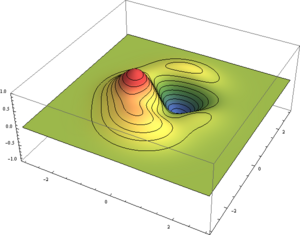
En resumen, existen multitud de opciones.
El problema aparece cuando se trata de visualizar campos dependientes de las tres coordenadas del espacio.
6 Enlaces
- Siguiente: Superficies equiescalares
- Anterior: Concepto de campo
